hdu5729
题意:
给你n行m列的网格图,对于一个网格图,他是不稳定的,因为他是四边形,允许你在四边形里面加边斜边,斜边有两种,加斜边之后当前格子变成两个三角形具有稳定性,当所有格子稳定时,称整个网格稳定。询问你有多少种加边的方法使得网格图稳定。
给你n行m列的网格图,对于一个网格图,他是不稳定的,因为他是四边形,允许你在四边形里面加边斜边,斜边有两种,加斜边之后当前格子变成两个三角形具有稳定性,当所有格子稳定时,称整个网格稳定。询问你有多少种加边的方法使得网格图稳定。
一方面:
先考虑网格不稳定的表现,发现有一些当前垂直的横边与竖边,不具有稳定性,有变得不垂直的可能。
再考虑网格稳定的表现,如果所有的横边与竖边永远保持垂直,那么网格稳定。
另一个方面:
先考虑网格不稳定的表现,发现有一些当前平行的横边间或竖边间,不具有稳定性,有变得不平行的可能。
再考虑网格稳定的表现,如果所有的横边间永远平行且竖边间永远平行且存在一条横边与竖边垂直,那么网格稳定。
总结:
当所有的横边间、竖边间永远平行,所有的横边与竖边永远垂直时,网格稳定。
不知道什么定理:
如果线段a平行于线段b,线段a垂直于线段c,那么线段b垂直于线段c。
如果线段a垂直与线段c,线段b垂直与线段c,那么线段a平行于线段b。
观察发现:
对于列位置相同的横边集,永远平行,对于行位置相同的竖边集,永远平行。
对根据上诉现象及分析,对边按照分类,列位置相同的边属于相同的集合,行位置相同的边属于相同集合。
然后考虑加斜边的影响:
每加入一条斜边,使得当前格子稳定。表现为使得当前格子的横边与竖边永远垂直。由(4)和(6)我们得到: 若命名:当前格子所在横边所属与的集合为a,当前格子所在竖边所属于的集合为b。 则集合a中所有边与集合b中所有边垂直。
如果我们用图(不一定是二分图)来表示这些集合之间的关系,将所有横边集组成集合A,将所有竖边集组成集合B,用图的边来表示垂直或平行关系,若边的顶点在集合内部,则边代表平行,否则代表垂直。用由(4)和(5)得出此无向图具有传递性。
当此图的传递闭包为完全图时,由(3)得出网格稳定。此命题等价于:若原图联通,则网格稳定。
于是原问题等价于:
给你集合A有n个点,集合B有m个点,有两种权值的无向边,可以添加到属于不同集合的点之间,问你有多少种加边方法可以让此图联通,
这时候我们才发现,其实不允许在集合内部加边,也就是说,此图的原型实际上为二分图
于是原问题等价于:
给你一个二分图,包含两个集合,集合A有n个点,集合B有m个点,允许添加两种权值的无向边,问你有多少种加边方法可以让此二分图联通。
对于新的问题,我们采取dp解决:
dp[i][j]代表左边i个点右边j个点的答案;
正面难以解决,考虑反面;
i+j个点的此二分图一共有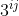 种,从左边拿一个点出来考虑;
种,从左边拿一个点出来考虑;
对于此点,分类讨论 ,考虑与它联通的所有其他点的数量,设左边有x个右边有y个,剩下的其他点自由组合,
于是 x的范围[0,i-1] y的范围[0,j];
这些类别全部加起来应该是全集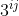
于是得到
![3^{ij}=\sum_{x=0}^{i-1}\sum_{y=0}^{j}(C_{i-1}^{x}*C_{j}^{y}*dp[x+1][y]*3^{(i-1-x)(j-y)})](https://latex.codecogs.com/gif.latex?3^{ij}=\sum_{x=0}^{i-1}\sum_{y=0}^{j}(C_{i-1}^{x}*C_{j}^{y}*dp[x+1][y]*3^{(i-1-x)(j-y)}))
得到dp式子:
![dp[i][j]=3^{ij}-\sum_{x=0}^{i-1}\sum_{y=0}^{j}(C_{i-1}^{x}*C_{j}^{y}*dp[x+1][y]*3^{(i-1-x)(j-y)}](https://latex.codecogs.com/gif.latex?dp[i][j]=3^{ij}-\sum_{x=0}^{i-1}\sum_{y=0}^{j}(C_{i-1}^{x}*C_{j}^{y}*dp[x+1][y]*3^{(i-1-x)(j-y)}) 当x等于i-1时y不取到j
当x等于i-1时y不取到j
先考虑网格不稳定的表现,发现有一些当前垂直的横边与竖边,不具有稳定性,有变得不垂直的可能。
再考虑网格稳定的表现,如果所有的横边与竖边永远保持垂直,那么网格稳定。
-------(1)
另一个方面:
先考虑网格不稳定的表现,发现有一些当前平行的横边间或竖边间,不具有稳定性,有变得不平行的可能。
再考虑网格稳定的表现,如果所有的横边间永远平行且竖边间永远平行且存在一条横边与竖边垂直,那么网格稳定。
-------(2)
总结:
当所有的横边间、竖边间永远平行,所有的横边与竖边永远垂直时,网格稳定。
-------(3)
不知道什么定理:
如果线段a平行于线段b,线段a垂直于线段c,那么线段b垂直于线段c。
-------(4)
如果线段a垂直与线段c,线段b垂直与线段c,那么线段a平行于线段b。
-------(5)
观察发现:
对于列位置相同的横边集,永远平行,对于行位置相同的竖边集,永远平行。
-------(6)
对根据上诉现象及分析,对边按照分类,列位置相同的边属于相同的集合,行位置相同的边属于相同集合。
然后考虑加斜边的影响:
每加入一条斜边,使得当前格子稳定。表现为使得当前格子的横边与竖边永远垂直。由(4)和(6)我们得到: 若命名:当前格子所在横边所属与的集合为a,当前格子所在竖边所属于的集合为b。 则集合a中所有边与集合b中所有边垂直。
如果我们用图(不一定是二分图)来表示这些集合之间的关系,将所有横边集组成集合A,将所有竖边集组成集合B,用图的边来表示垂直或平行关系,若边的顶点在集合内部,则边代表平行,否则代表垂直。用由(4)和(5)得出此无向图具有传递性。
当此图的传递闭包为完全图时,由(3)得出网格稳定。此命题等价于:若原图联通,则网格稳定。
于是原问题等价于:
给你集合A有n个点,集合B有m个点,有两种权值的无向边,可以添加到属于不同集合的点之间,问你有多少种加边方法可以让此图联通,
这时候我们才发现,其实不允许在集合内部加边,也就是说,此图的原型实际上为二分图
于是原问题等价于:
给你一个二分图,包含两个集合,集合A有n个点,集合B有m个点,允许添加两种权值的无向边,问你有多少种加边方法可以让此二分图联通。
对于新的问题,我们采取dp解决:
dp[i][j]代表左边i个点右边j个点的答案;
正面难以解决,考虑反面;
i+j个点的此二分图一共有
对于此点,分类讨论 ,考虑与它联通的所有其他点的数量,设左边有x个右边有y个,剩下的其他点自由组合,
于是 x的范围[0,i-1] y的范围[0,j];
这些类别全部加起来应该是全集
于是得到
得到dp式子:
#include <bits/stdc++.h> using namespace std; #define ll long long const ll mod = 1e9 + 7; ll C[20][20], dp[20][20], pow3[200]; int main() { pow3[0] = 1; for (int i = 1; i < 200; i++) pow3[i] = pow3[i - 1] * 3 % mod; C[0][0] = 1; for (int i = 1; i < 20; i++) { C[i][0] = 1; for (int j = 1; j <= i; j++) { C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % mod; } } for (int i = 0; i <= 10; i++) { for (int j = 0; j <= 10; j++) { dp[i][j] = 1000*mod+pow3[i*j]; for (int x = 0; x <= i - 1; x++) { for (int y = 0; y <= j; y++) { if (x == i - 1 && y == j)continue; dp[i][j] -= C[i - 1][x] * C[j][y] % mod*dp[x + 1][y] % mod*pow3[(i - 1 - x)*(j - y)] % mod; } } dp[i][j] %= mod; } } int n, m; while (~scanf("%d%d", &n, &m))printf("%lld\n", dp[n][m]); }