多项式

多项式在计算机中一般以数组方式储存，假设有一个多项式f(x)，并且x^i前面的系数为ai，那么显然我们恰好可以用一个数组a来描述这个多项式，多项式的系数ai恰好存在数组a的第i项a[i]；

多项式dft

在一般的多项式中，如果模数允许，乘法采取ntt来做，因为速度较快，多项式乘法是整个多项式体系的基石，他的常数如果太大，将影响到后面的所有的多项式操作，

多项式前期预处理

我们需要设置多项式最大长度，模数，原根，多项式最大长度的log，以及关键点reduce函数，传入一个-mod到mod之间的数x，返回x%mod,他比取模更快然后是快速幂，在往后是复数i在模意义下的值，2i在模意义下的逆元,以及后面的逆元数组和他的初始化函数

const int maxn=100005<<2,mod = 998244353,g=3;// const 能明显加速代码
const int lgmaxn=20;
#define reduce(x) ((x)+(((x)>>31)&mod))

int qpow(int a,int b){
    int ret=1;
    while(b){
        if(b&1) ret=1ll*ret*a%mod;
        a=1ll*a*a%mod;
        b>>=1;
    }
    return ret;
}

int I=86583718;
int inv2=qpow(2,mod-2);
int inv2I=qpow(2*I,mod-2);

int inv[maxn]={1,1};
void inv_ini(){
    for(int i=2;i<maxn;++i) inv[i]=1ll*(mod-mod/i)*(inv[mod%i])%mod;
}

dft

蝴蝶变化必须预处理出来，否则太慢，最前面的是蝴蝶变换r[i][j]数组，之后是ntt单位根wn数组和他的逆元数组。接着是ntt的数组的预处理函数以及ntt函数本体

int allr[maxn<<1],*r[30],ntt_wn[30],ntt_revwn[30]; // 特别详细，没啥其他可说的 
//https://wenku.baidu.com/view/b438a51cce84b9d528ea81c758f5f61fb7362826.html
void dft_ini(){ // ntt 高性能
    r[0]=allr;
    for(int n=1,bit=0;n<maxn;n<<=1,bit++){
        for(int i=0;i<n;++i)r[bit][i]=(r[bit][i>>1]>>1)|((i&1)<<(bit-1));
        r[bit+1]=r[bit]+n;
        ntt_wn[bit]=qpow(g,(mod-1)>>bit);// 单位根
        ntt_revwn[bit]=qpow(ntt_wn[bit],mod-2);//逆变换则乘上逆元
    }
}
void dft(int*a,int n,int bits,int opt){ // ntt 
    for(int i=0;i<n;++i) if(i<r[bits][i]) swap(a[i],a[r[bits][i]]);
    for(int k=1,bit=0;k<n;k<<=1,bit++){
        int wn=opt==1?ntt_wn[bit+1]:ntt_revwn[bit+1];
        for (int i=0;i<n;i+=(k<<1)){
            for (int j=0,w=1; j<k; j++,w=1ll*w*wn%mod){
                int x=a[i+j], y=1ll*w*a[i+j+k]%mod;
                a[i+j]=reduce(x+y-mod), a[i+j+k]=reduce(x-y);
            }
        }
    }
    if(opt==-1) for(int i=0;i<n;++i) a[i]=1ll*a[i]*inv[n]%mod;
}//1800ms+

多项式拓展与对齐

为了后期代码可观性良好，以及少写一些奇怪的代码，poly_cpy(int*a,int n,int*b,int exn)提供了多项式拷贝等操作，即将一个多项式拷贝到另外一个多项式，必须保证exn>=n ，即先将a[0...n-1]拷贝到b[0...n-1] 然后把b数组多余的部分清零。这里如果ab为同一个数组，就不必进行拷贝了。

void poly_cpy(int*a,int n,int *b,int exn){//
    if(a!=b)  memcpy(b,a,sizeof(b[0])*n);
    if(n<exn) memset(b+n,0,sizeof(b[0])*(exn-n));
}

多项式乘法

为了防止常数问题，这里依旧采取最简单的方式，不让数组发生过多的拷贝，我们只实现a*=b这一个步骤，不实现c=a*b这种，很套路的乘法，先变为点指表示法然后变为系数表示法即可

void poly_mul(int*a,int na,int*b,int nb){
    static int c[maxn];
    int exn=1,bits=0;
    while(exn<na+nb-1) exn<<=1,bits++;
    poly_cpy(a,na,a,exn);
    poly_cpy(b,nb,c,exn);
    dft(a,exn,bits,1);
    dft(c,exn,bits,1);
    for(int i=0;i<exn;i++) a[i]=1ll*a[i]*c[i]%mod;
    dft(a,exn,bits,-1);
}

多项式求逆

若两个多项式f和g，求出f*g然后让系数对mod取模，多项式忽略高于x^k次的项后等于1，则f和g互逆
这个地方很难以理解，因为有两个取模，所以会让很多初学者感到困惑，只要注意两个模是不同的，一个是系数对mod取模，另一个是多项式整体对x^k取模，即可整个算法采取牛顿迭代法来完成，很容易被数学归纳法证明，f(x)*g(x)===1(x^k,mod),当k等于1的时候，非常好得出结果，显然那时候g(x)至少需要 1项，即常数项，大于常数项的部分无效的，这个很容易证明，这一项等于f(x)的常数项的逆元。然后我们来根据f(x)*g(x)===1(x^k,mod)推出f(x)*g(x)===1(x^2k,mod) 的结果,以下是推导过程,显然g(x)=g(x)*(2-f(x)*g(x)),只要自己注意一下项数的变化即可，然后我们倍增即可得出答案时间复杂度T(n)=T(n/2)+nlg(n) 根据主定理T(n)=O(nlgn)

void poly_inv(int*a,int n,int*b){ //  // %(x^n)  b(2-ab)
    static int c[maxn];
    if(n==1) {b[0]=qpow(a[0],mod-2); return;}
    poly_inv(a,(n+1)>>1,b);
    int exn=1,bits=0;
    while(exn<n+n-1) exn<<=1,bits++;
    poly_cpy(b,(n+1)>>1,b,exn);
    poly_cpy(a,n,c,exn);
    dft(b,exn,bits,1);
    dft(c,exn,bits,1);
    for(int i=0;i<exn;i++) b[i]=b[i]*(2-1ll*c[i]*b[i]%mod+mod)%mod;
    dft(b,exn,bits,-1);
}//p4738 开O2 500ms+ 洛谷最快200ms+

多项式除法

除法会有剩余，所以有两个返回值。
对于一个n-1次多项式f(x) 定义F(x)=x^nf(1/x) 则有以下推导

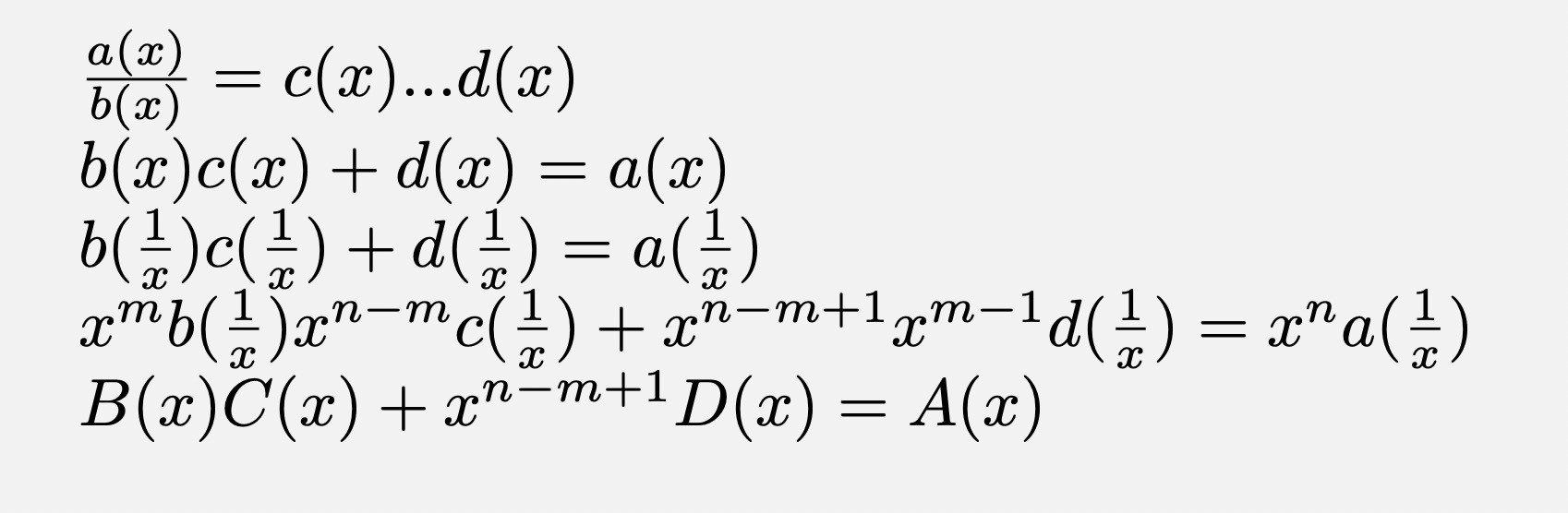
f到F只不过是系数翻转我们可以通过求逆迅速计算D(x) 继而的得到d(x) 余数直接ntt暴力即可

void poly_div(int*a,int na,int*b,int nb,int*c,int*d){
    reverse(a,a+na); reverse(b,b+nb);
    poly_inv(b,na-nb+1,c); //exn(2*na-2*nb+1)=exn(2*na-nb-nb+1)
    poly_mul(c,na-nb+1,a,na); //exn(na-nb+1+na-1)=exn(2*na-nb)
    reverse(a,a+na); reverse(b,b+nb);

    reverse(c,c+na-nb+1);
    poly_cpy(c,na-nb+1,d,na-nb+1);
    poly_mul(d,na-nb+1,b,nb);
    for(int i=0;i<na;i++) d[i]=reduce(a[i]-d[i]);
}// p4738 开O2 600ms+ 洛谷最快300ms+

多项式取对数

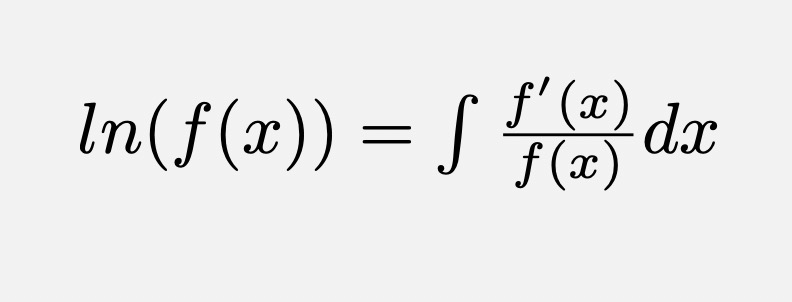
于是求导、求逆、乘、积分即可完成

void poly_der(int*a,int n,int*b){ // 微分求导
    for(int i=1;i<n;i++) b[i-1]=1ll*a[i]*i%mod;
}

void poly_int(int*a,int n,int*b){ // 默认积分结果项常的数为0
    for(int i=1;i<=n;i++) b[i]=1ll*a[i-1]*inv[i]%mod;
    b[0]=0;
}


void poly_ln(int*a,int n,int*b){// a[exn(n+n-1)] //保证f(0)=1 , 默认积分结果项常的数为0 ，b[0]=ln(a[0])=1
    static int d[maxn];
    poly_der(a,n,d); // n-1 
    poly_inv(a,n,b); // n
    poly_mul(d,n-1,b,n);
    poly_int(d,n,b); // b[0]=ln(a[0])=ln(1)=0
}//p4725 开O2 700ms+ 洛谷最快300ms+

多项式求指数函数

大佬已将讲的很清楚了，用泰勒展开求的

void poly_exp(int*a,int n,int*b){//a[exn(n+n-1)] // 保证f(0)=0 b(1-ln(b)+f), 
    static int a_lnb[maxn];
    if(n==1) {b[0]=1;return;}
    poly_exp(a,(n+1)>>1,b);
    poly_cpy(b,(n+1)>>1,b,n);
    poly_ln(b,n,a_lnb);
    for(int i=0;i<n;++i) a_lnb[i]=reduce(a[i]-a_lnb[i]);
    a_lnb[0]=reduce(a_lnb[0]+1-mod);
    poly_mul(b,n,a_lnb,n);
}//p4726 开O2 1600ms+ 洛谷最快400ms+

多项式开根

递归边界改为二次剩余即可

void poly_sqrt(int*a,int n,int*b){//a[exn(n+n-1)] //保证a[0]=1, (b+a/b)/2 比上面那个好一些 
    static int c[maxn];
    if(n==1) {b[0]=1;return;}
    poly_sqrt(a,(n+1)>>1,b);
    poly_cpy(b,(n+1)>>1,b,n);
    poly_inv(b,n,c);
    poly_mul(c,n,a,n);
    int inv2=qpow(2,mod-2);
    for(int i=0;i<n;i++) b[i]=1ll*(b[i]+c[i])*inv2%mod;
}// P5205 开O2 3200+ms 洛谷最快600ms++

多项式快速幂

先取对数，然后乘，然后取exp

void poly_pow(int *a,int n,int k,int *b){//a[exn(n+n-1)] // a^k not quick pow but quicker
    static int c[maxn],d[maxn];
    int t=0;
    while(t<n&&a[t]==0) t++;// a[t]*x^t
    if(1ll*t*k>=n)return; //k*t 居然能够爆int
    a+=t;// a/=x^t
    int invat=qpow(a[0],mod-2);
    int mul=qpow(a[0],k);
    for(int i=0;i<n-t;i++)d[i]=1ll*a[i]*invat%mod;
    for(int i=n-t;i<n;i++)d[i]=0;
    poly_ln(d,n,c);
    for(int i=1;i<n;i++)c[i]=1ll*c[i]*k%mod;
    poly_exp(c,n,b);
    for(int i=n-1;i>=1ll*t*k;i--) b[i]=1ll*b[i-1ll*k*t]*mul%mod;
    for(int i=1ll*k*t-1;i>=0;i--) b[i]=0;
    // b*=x^kt
}// 若k为大数，且保证a[0]=1，传入k%mod即可

多项式三角函数

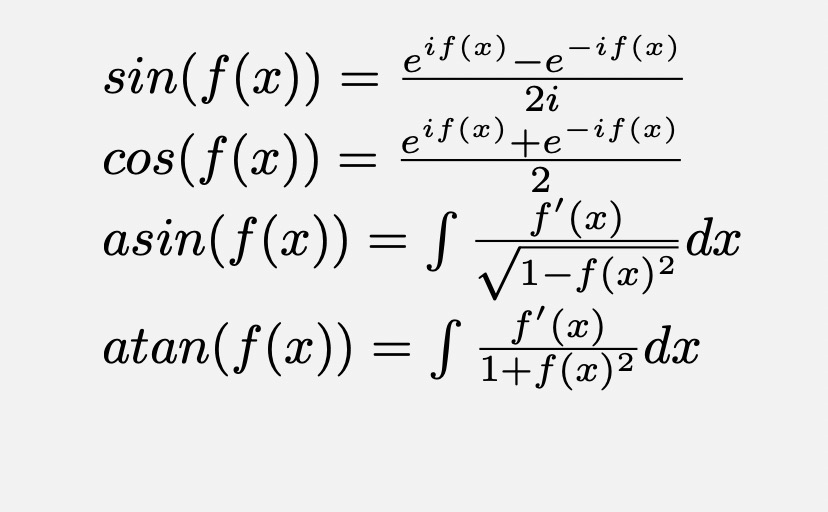
void poly_sin(int*a,int n,int*b){//a[exn(n+n-1)]// 保证a[0]=0 -> c[0]=0 -> 可以exp
    static int c[maxn],d[maxn];
    for(int i=0;i<n;i++) c[i]=1ll*a[i]*I%mod;
    poly_exp(c,n,b);
    poly_inv(b,n,d);
    for(int i=0;i<n;i++) b[i]=1ll*(b[i]-d[i]+mod)*inv2I%mod;
} //  P5264 开O2 2111ms 洛谷最快691ms

void poly_cos(int*a,int n,int*b){//a[exn(n+n-1)]// 保证a[0]=0 -> c[0]=0 -> 可以exp
    static int c[maxn],d[maxn];
    for(int i=0;i<n;i++) c[i]=1ll*a[i]*I%mod;
    poly_exp(c,n,b);
    poly_inv(b,n,d);
    for(int i=0;i<n;i++) b[i]=1ll*(b[i]+d[i])*inv[2]%mod;
}//  P5264 开O2 2111ms 洛谷最快691ms

void poly_asin(int*a,int n,int*b){//a[exn(n+n-1)]// 保证a[0]=0 积分： f'/(sqrt(1-f*f))
    static int c[maxn];
    poly_cpy(a,n,b,n);// f
    poly_mul(b,n,b,n);// f*f
    b[0]=reduce(b[0]-1);// f*f-1 
    for(int i=0;i<n;i++)b[i]=mod-b[i]; //1-ff
    poly_sqrt_Strong(b,n,c);// sqrt(1-ff)
    poly_inv(c,n,b); // 1/sqrt(1-ff)
    poly_der(a,n,c);// f'
    poly_mul(c,n,b,n);//
    poly_int(c,n,b);// f'/(sqrt(1-f*f))
}// P5265 开O2 1626ms 洛谷最快985ms

void poly_atan(int*a,int n,int*b){//a[exn(n+n-1)] // 保证a[0]=0 积分： f'/(sqrt(1-f*f))
    static int c[maxn];
    poly_cpy(a,n,b,n);// f
    poly_mul(b,n,b,n);// f*f
    b[0]=reduce(b[0]+1-mod);// f*f+1 
    poly_inv(b,n,c); // 1/(f*f+1)
    poly_der(a,n,b);// f'
    poly_mul(c,n,b,n);//
    poly_int(c,n,b);// f'/(f*f+1)
}// P5265 开O2 1626ms 洛谷最快985ms

拉格朗日插值法

。。。。。。没啥可说的，存粹的套路

多项式多点求值

完整代码

#include<bits/stdc++.h>
using namespace std;

const int maxn=100005<<2,mod = 998244353,g=3;// const 能明显加速代码
const int lgmaxn=20;
#define reduce(x) ((x)+(((x)>>31)&mod))

int qpow(int a,int b){
    int ret=1;
    while(b){
        if(b&1) ret=1ll*ret*a%mod;
        a=1ll*a*a%mod;
        b>>=1;
    }
    return ret;
}

int I=86583718;
int inv2I=qpow(2*I,mod-2);

int inv[maxn]={1,1};
void inv_ini(){
    for(int i=2;i<maxn;++i) inv[i]=1ll*(mod-mod/i)*(inv[mod%i])%mod;
}

int allr[maxn<<1],*r[30],ntt_wn[30],ntt_revwn[30]; // 特别详细，没啥其他可说的 
//https://wenku.baidu.com/view/b438a51cce84b9d528ea81c758f5f61fb7362826.html
void dft_ini(){ // ntt 高性能
    r[0]=allr;
    for(int n=1,bit=0;n<maxn;n<<=1,bit++){
        for(int i=0;i<n;++i)r[bit][i]=(r[bit][i>>1]>>1)|((i&1)<<(bit-1));
        r[bit+1]=r[bit]+n;
        ntt_wn[bit]=qpow(g,(mod-1)>>bit);// 单位根
        ntt_revwn[bit]=qpow(ntt_wn[bit],mod-2);//逆变换则乘上逆元
    }
}
void dft(int*a,int n,int bits,int opt){ // ntt 
    for(int i=0;i<n;++i) if(i<r[bits][i]) swap(a[i],a[r[bits][i]]);
    for(int k=1,bit=0;k<n;k<<=1,bit++){
        int wn=opt==1?ntt_wn[bit+1]:ntt_revwn[bit+1];
        for (int i=0;i<n;i+=(k<<1)){
            for (int j=0,w=1; j<k; j++,w=1ll*w*wn%mod){
                int x=a[i+j], y=1ll*w*a[i+j+k]%mod;
                a[i+j]=reduce(x+y-mod), a[i+j+k]=reduce(x-y);
            }
        }
    }
    if(opt==-1) for(int i=0;i<n;++i) a[i]=1ll*a[i]*inv[n]%mod;
}//1800ms+

void poly_show(int*a,int n){
    for(int i=0;i<n;i++) printf(" %dx^%d +",a[i]>1000?a[i]-mod:a[i],i);
    cout<<endl;
}

void poly_cpy(int*a,int n,int *b,int exn){//
    if(a!=b)  memcpy(b,a,sizeof(b[0])*n);
    if(n<exn) memset(b+n,0,sizeof(b[0])*(exn-n));
}

/* 
 a会被作拓展，但是b不会，所以b的范围不会改变
 a[exn(na+nb-1)] 
 a*=b a和b允许是同一个数组
*/
void poly_mul(int*a,int na,int*b,int nb){
    static int c[maxn];
    int exn=1,bits=0;
    while(exn<na+nb-1) exn<<=1,bits++;
    poly_cpy(a,na,a,exn);
    poly_cpy(b,nb,c,exn);
    dft(a,exn,bits,1);
    dft(c,exn,bits,1);
    for(int i=0;i<exn;i++) a[i]=1ll*a[i]*c[i]%mod;
    dft(a,exn,bits,-1);
}
/*
b会被作拓展，但是a不会，所以a数组传入没有任何数组大小的要求
b[exn(n+n-1)]
*/
void poly_inv(int*a,int n,int*b){ //  // %(x^n)  b(2-ab)
    static int c[maxn];
    if(n==1) {b[0]=qpow(a[0],mod-2); return;}
    poly_inv(a,(n+1)>>1,b);
    int exn=1,bits=0;
    while(exn<n+n-1) exn<<=1,bits++;
    poly_cpy(b,(n+1)>>1,b,exn);
    poly_cpy(a,n,c,exn);
    dft(b,exn,bits,1);
    dft(c,exn,bits,1);
    for(int i=0;i<exn;i++) b[i]=b[i]*(2-1ll*c[i]*b[i]%mod+mod)%mod;
    dft(b,exn,bits,-1);
}//p4738 开O2 500ms+ 洛谷最快200ms+


/*
a/b=c...d
只有cb有要求exn(2*na-nb)
*/
void poly_div(int*a,int na,int*b,int nb,int*c,int*d){
    reverse(a,a+na); reverse(b,b+nb);
    poly_inv(b,na-nb+1,c); //exn(2*na-2*nb+1)=exn(2*na-nb-nb+1)
    poly_mul(c,na-nb+1,a,na); //exn(na-nb+1+na-1)=exn(2*na-nb)
    reverse(a,a+na); reverse(b,b+nb);

    reverse(c,c+na-nb+1);
    poly_cpy(c,na-nb+1,d,na-nb+1);
    poly_mul(d,na-nb+1,b,nb);
    for(int i=0;i<na;i++) d[i]=reduce(a[i]-d[i]);
}// p4738 开O2 600ms+ 洛谷最快300ms+

void poly_der(int*a,int n,int*b){ // 微分求导
    for(int i=1;i<n;i++) b[i-1]=1ll*a[i]*i%mod;
}

void poly_int(int*a,int n,int*b){ // 默认积分结果项常的数为0
    for(int i=1;i<=n;i++) b[i]=1ll*a[i-1]*inv[i]%mod;
    b[0]=0;
}


void poly_ln(int*a,int n,int*b){// a[exn(n+n-1)] //保证f(0)=1 , 默认积分结果项常的数为0 ，b[0]=ln(a[0])=1
    static int d[maxn];
    poly_der(a,n,d); // n-1 
    poly_inv(a,n,b); // n
    poly_mul(d,n-1,b,n);
    poly_int(d,n,b); // b[0]=ln(a[0])=ln(1)=0
}//p4725 开O2 700ms+ 洛谷最快300ms+

void poly_exp(int*a,int n,int*b){//a[exn(n+n-1)] // 保证f(0)=0 b(1-ln(b)+f), 
    static int a_lnb[maxn];
    if(n==1) {b[0]=1;return;}
    poly_exp(a,(n+1)>>1,b);
    poly_cpy(b,(n+1)>>1,b,n);
    poly_ln(b,n,a_lnb);
    for(int i=0;i<n;++i) a_lnb[i]=reduce(a[i]-a_lnb[i]);
    a_lnb[0]=reduce(a_lnb[0]+1-mod);
    poly_mul(b,n,a_lnb,n);
}//p4726 开O2 1600ms+ 洛谷最快400ms+

void poly_sqrt(int*a,int n,int*b){//a[exn(n+n-1)] //保证a[0]=1, (b+a/b)/2 比上面那个好一些 
    static int c[maxn];
    if(n==1) {b[0]=1;return;}
    poly_sqrt(a,(n+1)>>1,b);
    poly_cpy(b,(n+1)>>1,b,n);
    poly_inv(b,n,c);
    poly_mul(c,n,a,n);
    int inv2=qpow(2,mod-2);
    for(int i=0;i<n;i++) b[i]=1ll*(b[i]+c[i])*inv2%mod;
}// P5205 开O2 3200+ms 洛谷最快600ms++

int sqrt_residue(int a){ // return sqrt(a)
    int b=rand()%mod;   //找一个非二次剩余数 b
    while(qpow(b,(mod-1)>>1)!=mod-1) b=rand()%mod;
    int s=mod-1,t=0; // mod-1 =2^t*s = s<<t
    while(!(s&1)) s>>=1,t++;
    int inv=qpow(a,mod-2);
    int x,k;
    for(x=qpow(a,(s+1)>>1),k=1;t-k!=0;k++){ //
        int invxx=1ll*inv*x%mod*x%mod;
        if(qpow(invxx,1<<(t-k-1))==mod-1){
            x=1ll*x*qpow(b,s<<(k-1))%mod;
        }
    }
    return min(x,mod-x);
}

void poly_sqrt_Strong(int*a,int n,int*b){//a[exn(n+n-1)] //强化版 不保证a[0]=1 但保证a[0]为二次剩余
    static int c[maxn];
    if(n==1) {b[0]=sqrt_residue(a[0]);return;}// 其实就这一行不一样
    poly_sqrt_Strong(a,(n+1)>>1,b);
    poly_cpy(b,(n+1)>>1,b,n);
    poly_inv(b,n,c);
    poly_mul(c,n,a,n);
    for(int i=0;i<n;i++) b[i]=1ll*(b[i]+c[i])*inv[2]%mod;
}// 开O2跑1900ms+ 洛谷最快800ms++

void poly_pow(int *a,int n,int k,int *b){//a[exn(n+n-1)] // a^k not quick pow but quicker
    static int c[maxn],d[maxn];
    int t=0;
    while(t<n&&a[t]==0) t++;// a[t]*x^t
    if(1ll*t*k>=n)return; //k*t 居然能够爆int
    a+=t;// a/=x^t
    int invat=qpow(a[0],mod-2);
    int mul=qpow(a[0],k);
    for(int i=0;i<n-t;i++)d[i]=1ll*a[i]*invat%mod;
    for(int i=n-t;i<n;i++)d[i]=0;
    poly_ln(d,n,c);
    for(int i=1;i<n;i++)c[i]=1ll*c[i]*k%mod;
    poly_exp(c,n,b);
    for(int i=n-1;i>=1ll*t*k;i--) b[i]=1ll*b[i-1ll*k*t]*mul%mod;
    for(int i=1ll*k*t-1;i>=0;i--) b[i]=0;
    // b*=x^kt
}// 若k为大数，且保证a[0]=1，传入k%mod即可

void poly_sin(int*a,int n,int*b){//a[exn(n+n-1)]// 保证a[0]=0 -> c[0]=0 -> 可以exp
    static int c[maxn],d[maxn];
    for(int i=0;i<n;i++) c[i]=1ll*a[i]*I%mod;
    poly_exp(c,n,b);
    poly_inv(b,n,d);
    for(int i=0;i<n;i++) b[i]=1ll*(b[i]-d[i]+mod)*inv2I%mod;
} //  P5264 开O2 2111ms 洛谷最快691ms

void poly_cos(int*a,int n,int*b){//a[exn(n+n-1)]// 保证a[0]=0 -> c[0]=0 -> 可以exp
    static int c[maxn],d[maxn];
    for(int i=0;i<n;i++) c[i]=1ll*a[i]*I%mod;
    poly_exp(c,n,b);
    poly_inv(b,n,d);
    for(int i=0;i<n;i++) b[i]=1ll*(b[i]+d[i])*inv[2]%mod;
}//  P5264 开O2 2111ms 洛谷最快691ms

void poly_asin(int*a,int n,int*b){//a[exn(n+n-1)]// 保证a[0]=0 积分： f'/(sqrt(1-f*f))
    static int c[maxn];
    poly_cpy(a,n,b,n);// f
    poly_mul(b,n,b,n);// f*f
    b[0]=reduce(b[0]-1);// f*f-1 
    for(int i=0;i<n;i++)b[i]=mod-b[i]; //1-ff
    poly_sqrt_Strong(b,n,c);// sqrt(1-ff)
    poly_inv(c,n,b); // 1/sqrt(1-ff)
    poly_der(a,n,c);// f'
    poly_mul(c,n,b,n);//
    poly_int(c,n,b);// f'/(sqrt(1-f*f))
}// P5265 开O2 1626ms 洛谷最快985ms

void poly_atan(int*a,int n,int*b){//a[exn(n+n-1)] // 保证a[0]=0 积分： f'/(sqrt(1-f*f))
    static int c[maxn];
    poly_cpy(a,n,b,n);// f
    poly_mul(b,n,b,n);// f*f
    b[0]=reduce(b[0]+1-mod);// f*f+1 
    poly_inv(b,n,c); // 1/(f*f+1)
    poly_der(a,n,b);// f'
    poly_mul(c,n,b,n);//
    poly_int(c,n,b);// f'/(f*f+1)
}// P5265 开O2 1626ms 洛谷最快985ms

int*segtree[maxn<<2],segtreebuf[maxn*lgmaxn];
void zeropoint_to_poly(int rt,int*a,int n){ // T(n)=2*T(n/2)+nlg(n)= nlg(n)
    static int t1[maxn];
    if(rt==1) segtreebuf[0]=1;// auto ini
    segtree[rt]=segtreebuf+segtreebuf[0];
    segtreebuf[0]+=n+1;

    if(n==1) segtree[rt][0]=mod-a[0],segtree[rt][1]=1;
    else{
        int mid=n>>1;
        zeropoint_to_poly(rt<<1,a,mid);
        zeropoint_to_poly(rt<<1|1,a+mid,n-mid);
        poly_cpy(segtree[rt<<1],mid+1,t1,mid+1);
        poly_mul(t1,mid+1,segtree[rt<<1|1],n-mid+1);
        poly_cpy(t1,n+1,segtree[rt],n+1);
    }
}

/*
已知x0 x1 x2 ...
已知f(x)=a0x^0+a1x^1+a2x^2+...
求b0=f(x0),f(x1),f(x2)...
zeropoint_to_poly(1,)
*/
void poly_to_point(int rt,int*a,int n,int*b,int bn,int*c){ //T(n)=2*T(n/2)+nlg(n)=nlg(n)
    static int buf[maxn<<3],*d=buf,f[maxn];
    if(bn<=200&&n<=200){
        for(int i=0;i<bn;i++){
            c[i]=0;
            for(int j=n-1;j>=0;j--) c[i]=(1ll*c[i]*b[i]+a[j])%mod;
        }
    }
    else{
        d+=n<<2;
        if(n>bn) {
            poly_div(a,n,segtree[rt],bn+1,f,d);// nlg(n) 
            a=d; n=bn;
        }
        int mid=bn>>1;
        poly_to_point(rt<<1,a,n,b,mid,c);
        poly_to_point(rt<<1|1,a,n,b+mid,bn-mid,c+mid);
        d-=n<<2;
    }
}//时间卡边界上，不过刚刚好

//  拉格朗日插值法 
int facinv[maxn]={1,1};
void facinv_ini(){
    for(int i=0,fac=1;i<maxn;++i,fac=1ll*fac*i%mod) {
        facinv[i]=qpow(fac,mod-2);
    }
}

int lagrange(int*x,int*y,int n,int var){// y=f(x) 已知f(x0) f(x1) ... f(xn) 计算 f(var) O(n^2)
    int b=0;
    for(int i=0;i<=n;++i) {
        int t1=1,t2=1;
        for(int j=0;j<=n;j++){
            if(i==j) continue;
            t1=1ll*t1*(var -x[j]+mod)%mod;
            t2=1ll*t2*(x[i]-x[j]+mod)%mod;
        }
        int invt2=qpow(t2,mod-2);
        b=(b+1ll*y[i]*t1%mod*invt2)%mod;
    }
    return b;
}


int lagrange(int *y,int n,int x){// O(n) n次多项式有n+1项 y[0]...y[n] -> y[x]
    static int prepre[maxn],suf[maxn],*pre=prepre+1;
    pre[-1]=suf[n+1]=1;
    for(int i=0;i<=n;++i) pre[i]=1ll*pre[i-1]*(x-i+mod)%mod;
    for(int i=n;i>=0;i--) suf[i]=1ll*suf[i+1]*(i-x+mod)%mod;
    int b=0;
    for(int i=0;i<=n;++i) {
        int up=1ll*pre[i-1]*suf[i+1]%mod;
        int down=1ll*facinv[i]*facinv[n-i]%mod;
        b=(b+1ll*y[i]*up%mod*down)%mod;
    }
    return b;
}

// 
void lagrange_dfs(int rt,int*x,int n,int*g,int*a){
    static int buf[maxn<<4],*b=buf;
    b+=n<<2;
    if(n==1) a[0]=g[0];
    else{
        int mid=n>>1;
        lagrange_dfs(rt<<1,x,mid,g,a);
        lagrange_dfs(rt<<1|1,x+mid,n-mid,g+mid,b);
        poly_mul(a,mid,segtree[rt<<1|1],n-mid+1);
        poly_mul(b,n-mid,segtree[rt<<1],mid+1);
        for(int i=0;i<n;i++) a[i]=reduce(a[i]+b[i]-mod);
    }
    b-=n<<2;
}

void lagrange(int*x,int*y,int n,int *a){ // 多项式插值到系数表示法
    static int b[maxn],c[maxn]; // yi/gi*pord(x-xj) j!=i
    zeropoint_to_poly(1,x,n);
    poly_der(segtree[1],n+1,b);// b-> h'
    poly_to_point(1,b,n,x,n,c);//c->h'(x) 多点求值 洛必达法则
    for(int i=0;i<n;i++) c[i]=1ll*y[i]*qpow(c[i],mod-2)%mod;
    zeropoint_to_poly(1,x,n);
    lagrange_dfs(1,x,n,c,a);
}

inline int read(){
    register int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
    return (f==1)?x:-x;
}


int a[maxn],b[maxn],c[maxn],x[maxn],y[maxn];
int main(){
    dft_ini();inv_ini(); // all_poly
    // facinv_ini();// 简单的lagrange需要，复杂的不需要

    int n=read();
    for(int i=0;i<n;++i) a[i]=read();
    poly_ln(a,n,b);
    for(int i=0;i<n;i++) printf("%d ",b[i]);
}