三叉搜索树
ternary search tree
字典树的缺点
不难想到,对于那些字符集特别大的字典树来说,他们的空间消耗特别大,因为每个节点都要储存大量的指针,而这些指针往往又是空的。 # 将BST与trie结合起来 考虑这样一种树,每个节点有三个儿子,左右儿子表示自己的左右兄弟,向下的儿子表示真正的儿子。这样的树,将极大的提高了空间利用率。 # 偷个图来放着 这里插入了as,at,be,by,he.... 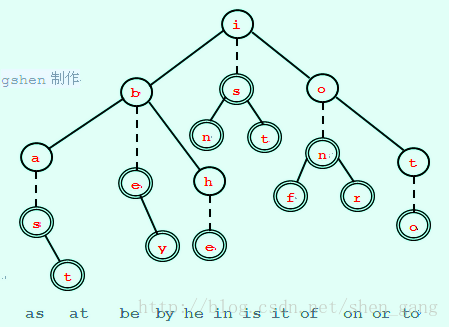
三叉搜索树的插入
考虑递归,假设我们插入到了某个节点,若下儿子与当前字符相等,则递归到下儿子并使用下一个字符来递归,如果当前字符小于下儿子,则递归到左儿子,保持当前字符不变,如果当前节点不存在了,则创建新节点,直接向下儿子走。
三叉搜索树的删除
我们还是用数字来记录终结节点的终结字符串有多少个,若找到待删除的节点以后,终止与此的只有一个字符串,则直接删掉,否则让终极节点的计数器减1,注意在回溯的时候,如果三个儿子都没有终结字符了,就删掉自己。
三叉搜索树的查找
递归递归。
三叉搜索树的缺点
树的平衡是一个很大的问题,这个我也没办法
三叉搜索树的本质
很多时候,很多数据结构像变戏法一样,我们从本质看带三叉搜索树,我们发现下儿子其实是字典树的边,在考虑左右儿子,其实这个就是bst,哈哈哈发现了没有, 我们考虑删掉所有下儿子,你会发现,剩下的是一个bst森林,就像lct删掉指向父亲没有指向自己的边以后,就是splay森林一样,很神奇。我们将这些bst森林转化为一个一个普通的数组,让这些数组从新充当节点,然后将下儿子连回去, 一切都清晰了,又变成普通字典树了。 所以三叉搜索树的本质是优化后的字典树,每个节点都是一个bst。即trie套bst,外层树为trie,内层树为bst。
三叉搜索树的优化?
我们让这里的bst用avl代替?用rbt代替?用sbt代替?都可以,但是我觉得这样编码太难了吧,若实在是真的差这点效率,可以去这样做,但我认为,把普通字典树的节点用avl-map、rbt-map、sbt-map直接范型编程或设为类中类不香吗。在这玩树套树确实高大上,效率也高,但编码难度也太高了。
代码
先欠着,以后再还。