lct
2019年8月5日
转移自老blog
在本质上他属于一种树剖分,将树剖成链,但是由于树是动态的,所以无法使用轻重剖分 ,因为重儿子可能会变化为轻儿子,轻儿子也可能变成重儿子,这里采取虚实剖分,按照虚链实链剖成链。
对于一般路径而言,我们直接强制换根来解决
操作1:把实边变为虚边,对应到链上 就是把一条链切断,在数据结构中体现为分裂
操作2:把实边变为虚边,对应到链上 就是把两条链合并,在数据结构中体现为合并
操作3:换根?这个较复杂,暂时不考虑
操作4:路径询问,在数据结构中体现为 整个数据结构维护的序列的性质,也即全段区间询问。
操作5:路径修改,在数据结构中体现为 整个数据结构维护的序列的性质,也即全段区间修改。
splay可以胜任,它支持分裂合并以及区间询问、修改,如果我们把整条链放入splay,用其中序遍历结果来 维护链,每一个splay再记录一个父亲,也即是此splay维护的链的父亲是谁?定义:链的父亲为链上深度最小的节点的父亲。,可以 证明,这些信息合并起来,对应到树是唯一的,于是问题基本解决
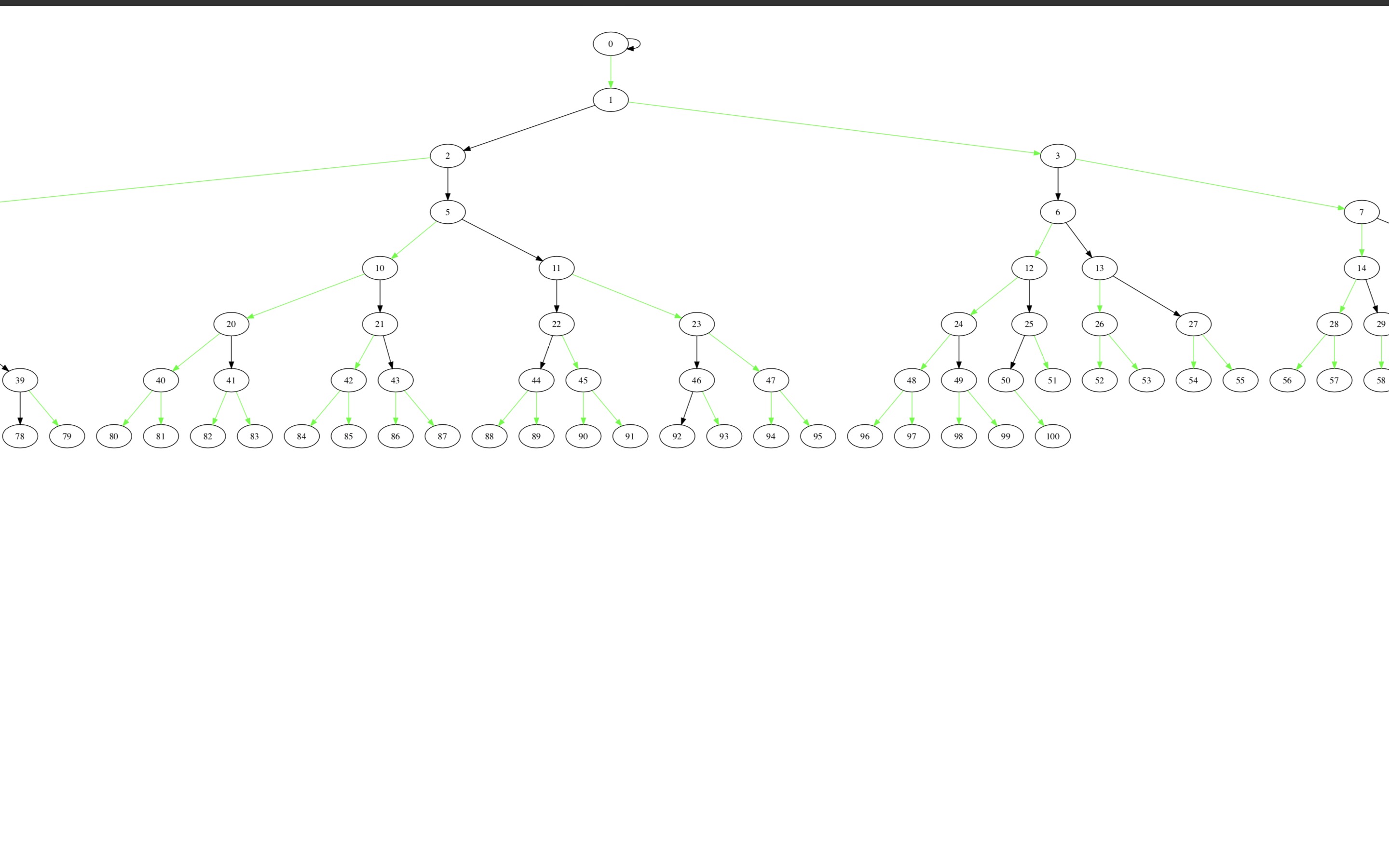
现在我们来考虑换根,换根是怎么一回事?我们来看上文的最后一张图,根为1,如果我们想把根换为44,怎嘛办呢? 如果你足够聪明,是可以想到做法的,实际上我们只需要将链1->2->5->11->22->44反转即可。证明过程很简单,此处不做证明。
至此,lct流程基本阐述完成,后面讲解细节操作。
link cut tree
link cut tree是什么
link cut tree是一种维护动态森林的数据结构,但我们常常用它来维护 一颗动态的树,维护这些动态树上路径的信息。在本质上他属于一种树剖分,将树剖成链,但是由于树是动态的,所以无法使用轻重剖分 ,因为重儿子可能会变化为轻儿子,轻儿子也可能变成重儿子,这里采取虚实剖分,按照虚链实链剖成链。
树的虚实剖分
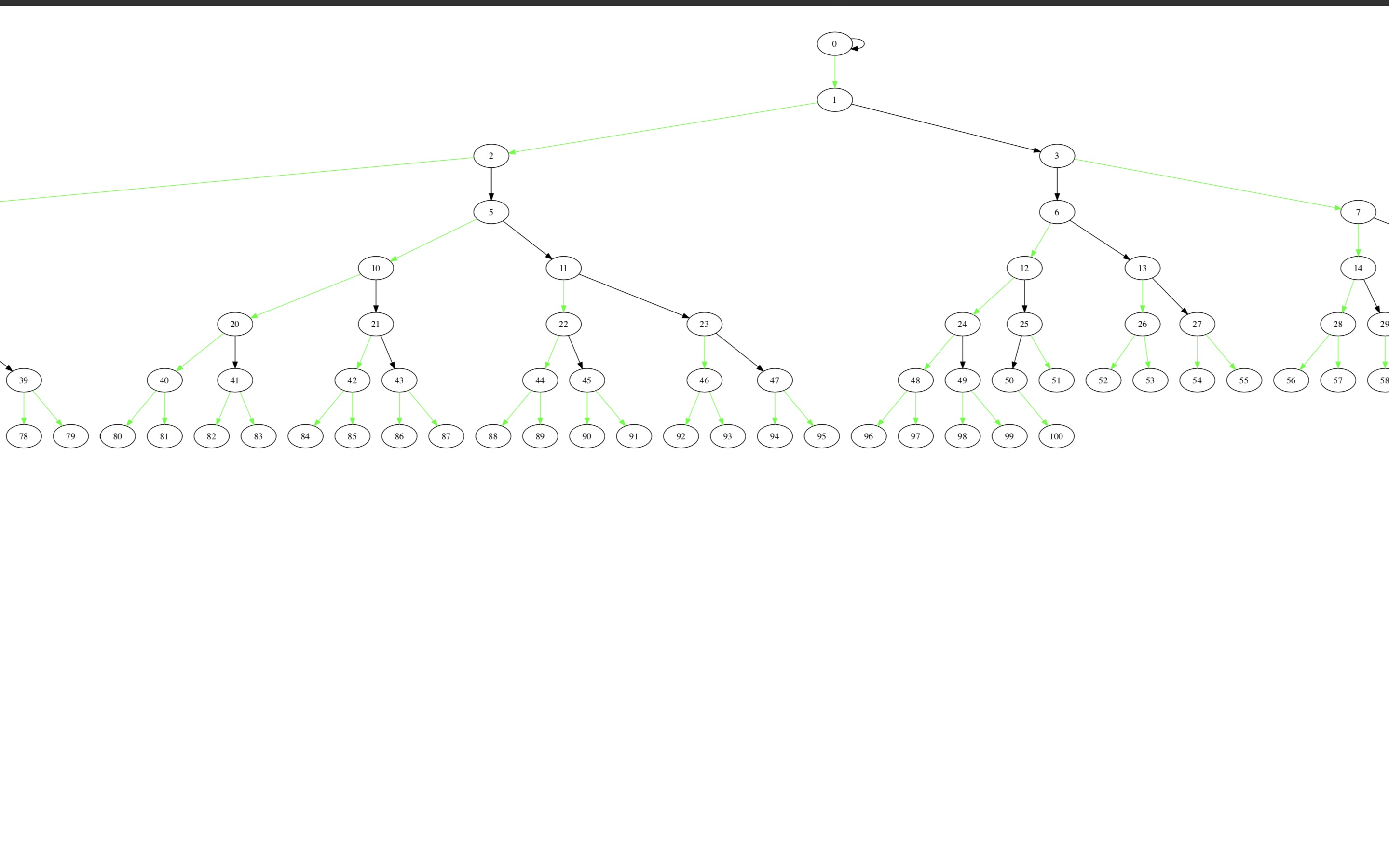
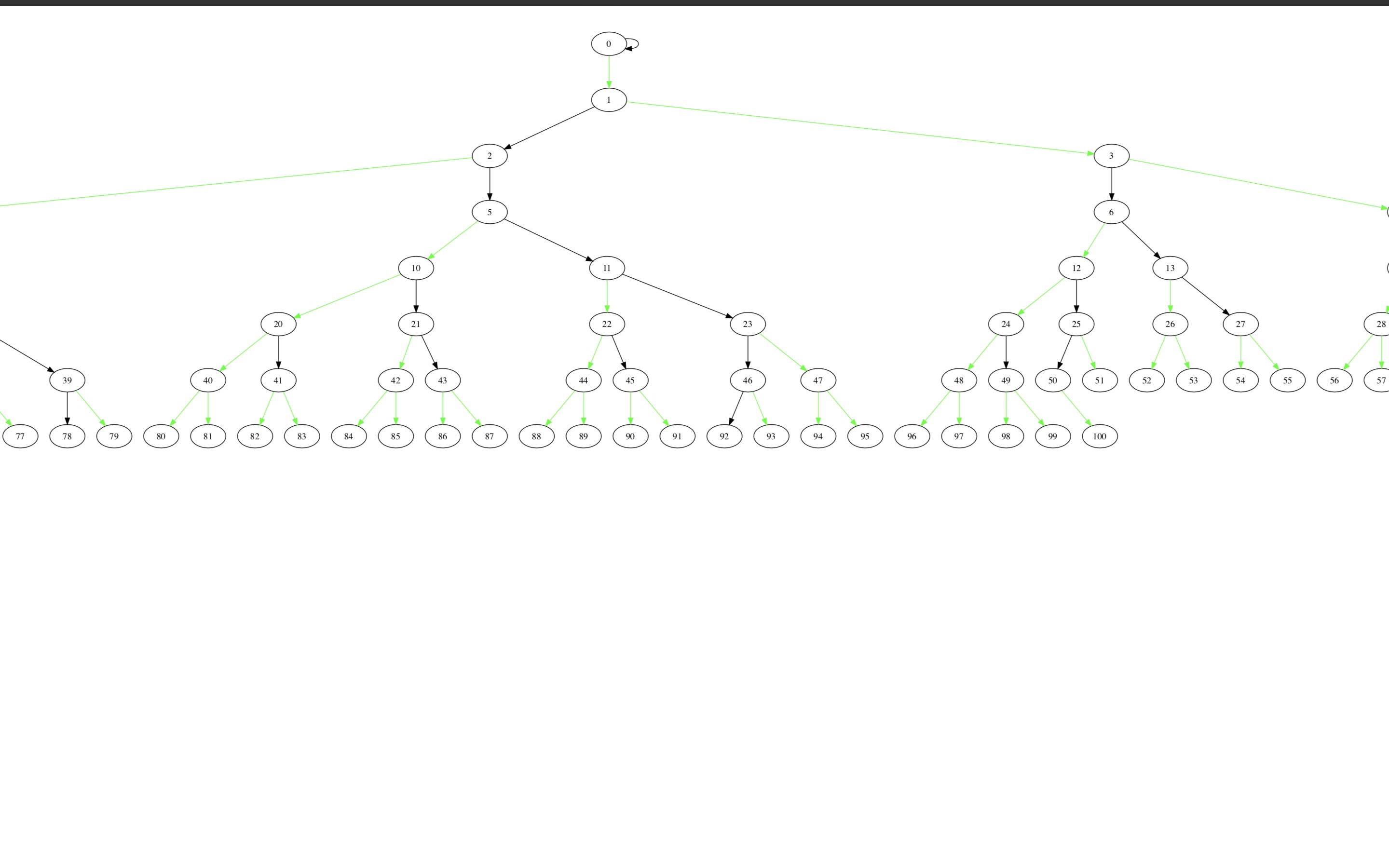
一个节点最多有一个实儿子,当然他也可以不拥有实儿子,除实儿子以外,其他儿子 被称作轻儿子。于是我们就像轻重剖分一样,把这棵树给剖掉了。这样剖,特别武断,看似无法保证时间复杂度,然而并非如此。证明过程较难,此处不做 描述。下面三张图都是二叉堆的虚实剖分,黑色边为实链,绿色为虚链


如何让被虚实剖分树具有动态
因为实儿子的选取限 制少,所以任何节点都有可能成为实儿子,当一棵树的形态发生了变化, 这并不影响我们的剖分,显然断边不会让我们的剖分出现任何问题,故而我们什么都不需要做,连边的话,无脑另此边为虚边即可。于是树的动态性不会影响 剖分如何维护路径信息
此问题较复杂,我们先考虑根到某个节点的路径,我们是这样做的,变换虚实边,使得 经过根的实链的两个端点分别是根和那个节点。可以证明,这样的剖分存在。变换虚实边之后,那条路径就被我们剖了出来,链是由数据结构来维护的, 于是我们就可以解决该路径问题了。对于一般路径而言,我们直接强制换根来解决
我们该选取何种数据结构
先来总结一下操作操作1:把实边变为虚边,对应到链上 就是把一条链切断,在数据结构中体现为分裂
操作2:把实边变为虚边,对应到链上 就是把两条链合并,在数据结构中体现为合并
操作3:换根?这个较复杂,暂时不考虑
操作4:路径询问,在数据结构中体现为 整个数据结构维护的序列的性质,也即全段区间询问。
操作5:路径修改,在数据结构中体现为 整个数据结构维护的序列的性质,也即全段区间修改。
splay可以胜任,它支持分裂合并以及区间询问、修改,如果我们把整条链放入splay,用其中序遍历结果来 维护链,每一个splay再记录一个父亲,也即是此splay维护的链的父亲是谁?定义:链的父亲为链上深度最小的节点的父亲。,可以 证明,这些信息合并起来,对应到树是唯一的,于是问题基本解决
现在我们来考虑换根,换根是怎么一回事?我们来看上文的最后一张图,根为1,如果我们想把根换为44,怎嘛办呢? 如果你足够聪明,是可以想到做法的,实际上我们只需要将链1->2->5->11->22->44反转即可。证明过程很简单,此处不做证明。
至此,lct流程基本阐述完成,后面讲解细节操作。
核心操作access
函数access(x),被调用后,我们会让起点在根,终点在x的链剖出,此链为过根节点的实链。操作很简单,我们 先将x伸展到它所在的那个splay的根,然后将它和他的右子树断开,为什么呢?因为他的右子树绝不在我们要的实链上,然后将它合并到此链的父亲上,但是此链的父亲可能已经有了 实儿子,那我们就将它断开,然后在把x子树合并上去,虽然是这么说的但是我们实际代码确实先合并子树,然后断链,其实是一样的。然后对其父亲作此操作,就结束了后面的其他没啥技术含量,也特别简单,就不讲了,代码如下
struct Link_Cut_Tree{ static const int N=1e5+555; int top,c[N][2],fa[N],xr[N],sta[N],rev[N],val[N]; void init(int n){ memset(fa,0,n<<2); memset(rev,0,n<<2); memset(c,0,n<<3); } inline void pushup(int x){xr[x]=xr[c[x][0]]^xr[c[x][1]]^val[x];} inline void pushdown(int x){ int l=c[x][0],r=c[x][1]; if(rev[x]){ rev[l]^=1;rev[r]^=1;rev[x]^=1; swap(c[x][0],c[x][1]); } } inline bool isroot(int x){return c[fa[x]][0]!=x&&c[fa[x]][1]!=x;} void rotate(int x){ int y=fa[x],z=fa[y],xis=c[y][1]==x,yis=c[z][1]==y;// if(!isroot(y))c[z][yis]=x;//son fa[x]=z;fa[y]=x;fa[c[x][xis^1]]=y;//father c[y][xis]=c[x][xis^1];c[x][xis^1]=y;//son pushup(y);pushup(x); } void splay(int x){ top=1;sta[top]=x;//init stack for(int i=x;!isroot(i);i=fa[i])sta[++top]=fa[i];//update stack for(int i=top;i;i--)pushdown(sta[i]);//pushroad while(!isroot(x)){ int y=fa[x],z=fa[y]; if(!isroot(y)){ if((c[y][0]==x)^(c[z][0]==y))rotate(x); else rotate(y); }rotate(x); } } void access(int x){for(int t=0;x;t=x,x=fa[x])splay(x),c[x][1]=t,pushup(x);} int treeroot(int x){access(x);splay(x);while(c[x][0])x=c[x][0];return x;} void makeroot(int x){access(x);splay(x);rev[x]^=1;} void cut(int x){access(x);splay(x);fa[c[x][0]]=fa[x];c[x][0]=0;fa[x]=0;}//cut the subtree x and let x to be the root void link(int x,int y){makeroot(x);fa[x]=y;} }tr;