树形dp
- 给你一棵n个节点的树,要你求出包含每个点的连通点集的数量。答案对1e9+7取模。
两次dfs,第一次处理每个节点的子孙方向的联通点集数量,
$$
dp[i]=\prod _{all..son}{(dp[son]+1)}
$$
第二次处理父亲方向的点集数量
$$
\begin{aligned}
&dp2[i] \
=&(\prod _{all..brother}{(dp1[brother]+1)})*dp2[father]+1 \
=&\frac{dp1[father]}{dp1[i]+1}*dp2[father]+1 \
\end{aligned}
$$
特别注意这里小心没有逆元
排序算法比较
1 |
|
Manacher算法
1 | struct Manacher {//鉴于马拉车算法较复杂,此处有少量修改, |
回文自动机
回文自动机,就像AC自动机一样,他采取字典树来储存状态集合,也像AC自动机是KMP 算法与字典树结合一样,回文自动机就是manacher算法和字典树结合的新算法。
在回文自动机里面,状态指的是,以字典树上所表示的字符串的逆序串的以末端字符镜像对称后得到的新串,简单说,baab在字典树上为root->a>b,cacaacac在字典树上为root->a->c->a->c,想像根就是对称中心,往儿子走就意味着,在对称中心两端加上同样的数字。当然这样子是无法表示奇数回文的,所以我们设立两个根就可以了。一个串的回文自动机,储存了这个串的所有回文子串。
回文自动机的状态转移的依据是回文,举个例子,如下图,如果黑色串代表以黄色字符为结尾 的最长的回文串,红色串代表黑色串的最长真后缀回文串,(定义:若回文串a为某串b的真后缀,则a为b的真后缀回文串,定义:若后缀a为某串b的后缀且 a!=b,则a为b的真后缀)当我们在黑串后面加上一个绿字符形成新串的时候,(姑且叫他黑绿串)回文自动机中的节点会发生什么样的变化呢?显然增加了 某些新的回文串,但是我们考虑这样一个事实,如果我们把黑绿串的最长后缀回文串加入到自动机中以后,我们就把黑绿串新增的所有回文串都可以被回文自动机所表示,证明类似于manacher算法,请自行证明。
下面来讨论如何把它加进去。我们假设粉色字符刚好是是红色串前的一个字符,如果粉色字符和绿色 字符为同一个字符的时候,我们可以肯定,黑绿串的最长真后缀回文串就是粉色字符+红串+绿色字符。此刻我们只需要新增一个节点了。如果他们不相等的话,重复 我们对黑串的算法与红串之上即可解决。
然后我们来考虑新增节点的所表示的回文后缀的最长真后缀回文串,我们重复使用上一段的算法,即可找到。
1 | struct palindrome_tree{ |
错位比较
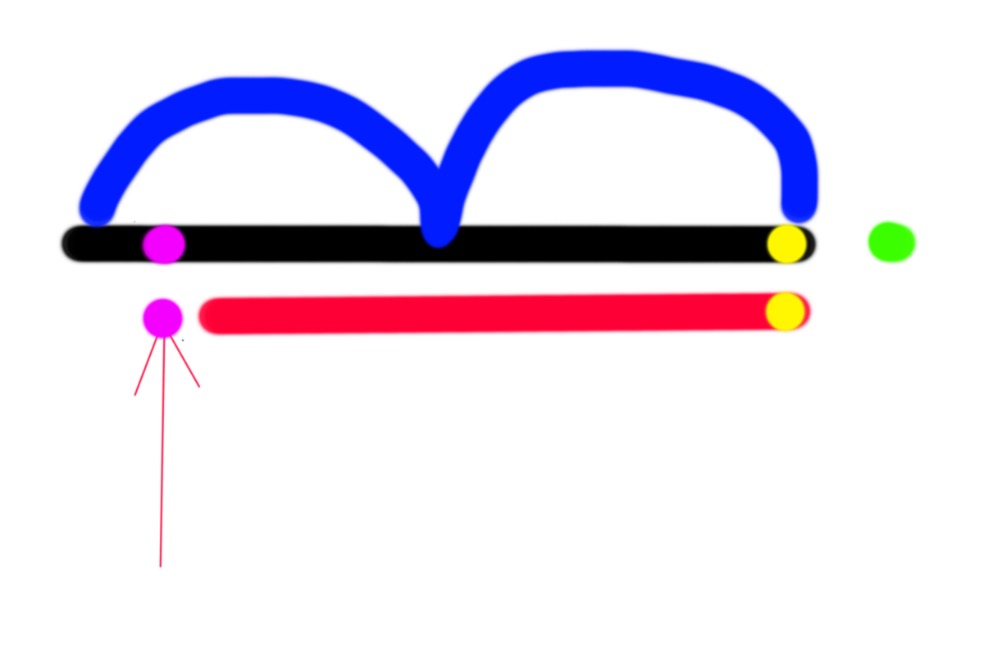
本质上让你求一个字符串可能的循环节,题目的第二个样例可以看作求序列 1,2,2,1,2,的循环节显然可以是3或5, 于是算法出来了,我们只要求出最小的循环节就可以了,最小的循环节怎么来求呢,我们hash预处理原字符串以便后面O1查询区间hash值,对于字符串s如下图,我们对原字符串复制一份,错位比较红色竖线之间的子串,如果相等,意味着什么读者可以自行思考,于是我们已经找到了On的做法了,我们只要从小到大枚举 蓝色区域即可
)
后缀数组
定义:
先定义一个字符串s,假设它的长度为n,s[i]表示第i个元素 ,s[i…]代表以s[i]开头且包含s[i]的后缀。我们定义新的数组 sa[i]为一个0-n的排列,且sa[i]为后缀s[i…]在所有后缀中按 照从小到大排序的排名。最后定义rank是sa的反函数。
sa数组也称为后缀数组
1 | //定义以s[i]开头的后缀是suf(i) |
FFT
题目1
给你类似剪刀石头布游戏的五种手势和十种克制关系。每种手势克制其他两种手势并被另外两种手势克制。给你两个字符串分别表示A,B的 手势顺序,A长B短,你可以随意挪动B相对于A的位置,求B最多能赢多少次?
1 | 若两个串为abcde和ede |
题目2
给你两个字符串原串和匹配串,串里只包含小写字母和∗,∗可以表示任意字符,问匹配串在原串不同位置中出现多少次,起始位置不同即不同位置。
我们还是利用上一题逆置短串构造卷积的方法,我们把*的值当作赋为0,pow(str1[i]−str2[i],2)*str1[i]*str2[i] 化简消去负数项即可
FFT
1 | const int maxn=4e6//开四倍所有数组。准确的数值是乘法结果数组的2进制对齐那么大。这个值小于四倍, |
NTT
1 | typedef long long ll; |
二分图最小费用固定流
这是我自己给这类图取的名字
给出定义, 有五类边
第一类为原点到左边的点,容量无穷大,有费用
第二类为左边的点到右边的点,一对一,容量为任意常数,费用0
第三类为右边的点到汇点,容量无穷大,费用0
第四类为左边的点依次连i->i+1,容量无穷大,费用0
第五类从右边连向左边,容量无穷大,费用0
如下图左边的图 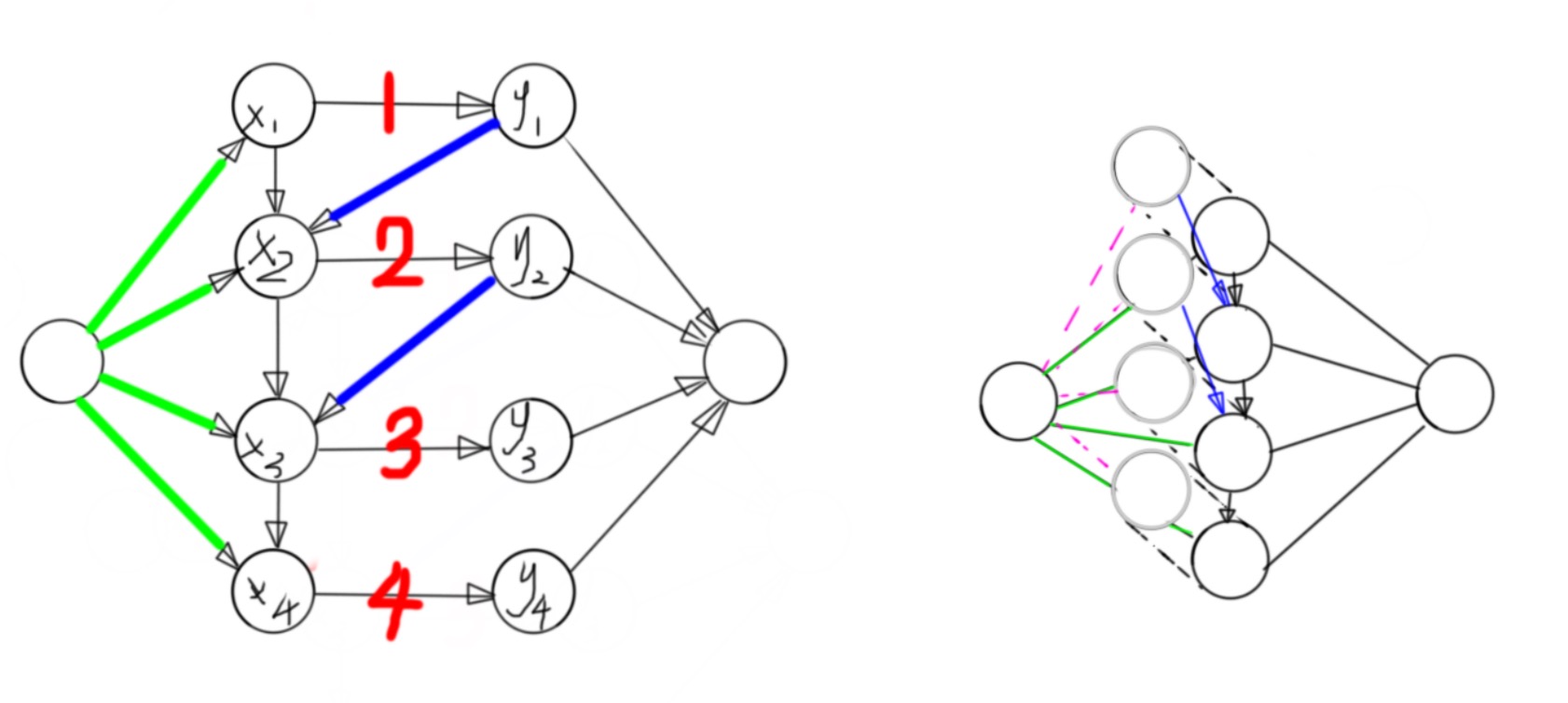
给出问题,求当有容量的边的都满流时的最小费用
我们发现左图的最大流一定满足有容量的边是满流的,我们尝试将其转化为最小费用最大流 我们发现,如果我们对左边的图跑最大流,当左边的图有流量进入y点集的时候,他一定会进 入源点,不会流回x点集,这就很烦,我们要的不是最大流,而是指定边的满流,我们尝试“阻 止”这个过程,怎么阻止呢,我们在考虑一个z点集,从源点出发,每当y点集有流量流入汇点,就从源点流等量流量到对应的z点集,我们最后用z点集完全替代y点集的回流功能,这样以后, 最小费用最大流就成了我们要求的最小费用固定流。
再仔细想想,我们发现y点集已经没有作用了,删掉他们,最后成了上图的右边的图。 于是解决了。
对于流入汇点的流量,我们可以构造一个新的点集,每当有流量流入汇点,我们就从源点流入 新的点集,实现回流机制。