kernel functions
核函数是一个函数,他能够把低纬空间映射到高维空间,他的输入是低维空间的两个点,他的输出是这两个点在高维空间上的内积。
why kernel functions
某些在低维空间无法使用超平面分割的点集,他们被某些函数映射到高维空间以后,能够被超平面分割。并且在高维空间中计算他们的内积很容易(就是核函数)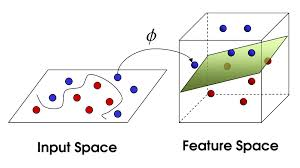
应用
Simple Example: x = (x1, x2, x3); y = (y1, y2, y3). Then for the function f(x) = (x1x1, x1x2, x1x3, x2x1, x2x2, x2x3, x3x1, x3x2, x3x3), the kernel is K(x, y ) = (<x, y>)².
Let’s plug in some numbers to make this more intuitive: suppose x = (1, 2, 3); y = (4, 5, 6). Then:
f(x) = (1, 2, 3, 2, 4, 6, 3, 6, 9)
f(y) = (16, 20, 24, 20, 25, 30, 24, 30, 36)
<f(x), f(y)> = 16 + 40 + 72 + 40 + 100+ 180 + 72 + 180 + 324 = 1024
A lot of algebra, mainly because f is a mapping from 3-dimensional to 9 dimensional space.
Now let us use the kernel instead:
K(x, y) = (4 + 10 + 18 ) ^2 = 32² = 1024
Same result, but this calculation is so much easier.
- 本文作者: fightinggg
- 本文链接: http://fightinggg.github.io/yilia/yilia/Q2G0IL.html
- 版权声明: 本博客所有文章除特别声明外,均采用 MIT 许可协议。转载请注明出处!



