X快速前缀树
我以前就说过,当你的数据结构达到了一定的基础,就可以学习那些更加高级的数据结构了,往往那些更加高级的数据结构由基本数据结构组合而成。
先提出一个问题
现在要你维护一个多重集合,支持3种操作,1询问一个值(这个值不一定在集合中)的前驱和后继,2向集合中插入一个元素,3从集合中删掉一个元素,1操作$10^6$次,2操作$10^5$次,3操作$10^5$,要求你在1S内完成回答。保证集合元素都小于M=$10^6$
普通平衡树?
我们考虑到上面三种操作都是普通平衡树常见的操作,很多人可能就直接拿起他自己的平衡树上了。很遗憾,大概率是无法通过的。因为操作次数太多了。
观察,思考
我们的操作需要的是大量的查询,大量、大量,你个普通平衡树怎么操作的过来?
新的平衡树
现在我们提出一个新的平衡树,这个平衡树非常厉害,他支持$O(lgM)$的时间来删除和插入,支持$O(lglgM)$的时间来查询前驱后继。
X快速前缀树
字典树+哈希表+维护叶子节点的双向链表+二分
首先,我们先建立一颗普通的01字典树,这个树我们对他稍作修改,考虑到字典树的节点分3类: 叶子节点、根节点、内部节点,我们让叶子节点间构造双向环状链表,其次,对于仅有左儿子的内部节点,让其右儿子指向子树的最小叶子节点,对于仅有右儿子的内部节点,让其左儿子指向子树的最大叶子节点。另一方面,我们对字典树的每一层都建立一个hash表,hash掉他们节点所代表的值是有还是没有,这样我们就构造出了一个X快速前缀树的模型了。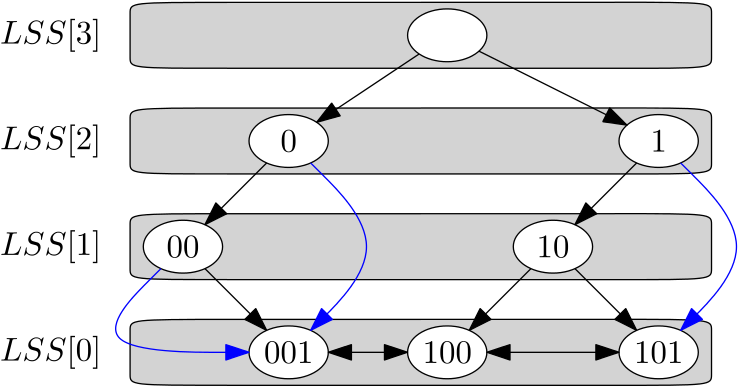
X快速前缀树的查找
假设我们要找一个数k,我们在树上寻找树和k的lca[最低公共祖先],这个过程可以只要在hash表中二分即可知道lca在哪一个节点,可以证明,这个节点要么没有左儿子,要么没有右儿子。如果有的话,他的儿子和k的lcp[最长公共前缀]一定更长,但是这与他自己是lca的事实相悖。另一方面,由于我们的单儿子节点储存了最值信息,如果这个节点没有右儿子,则他的右儿子指向的值是k的前驱,至于后继,在叶子节点的链表上后移一个单位即可。这个过程总复杂度在二分lca上,树的高度为lgn,二分高度,所以总体复杂度为$O(lglgn)$
X快速前缀树的插入
找出lca,若lca没有右儿子,则说明当前节点要插入到右儿子里面。照着做就行了,同时注意向下递归的时候把值也插入到hash表里面,递归到叶子的时候重新连接双向环状链表(前驱和后继),最后回溯的时候维护单儿子节点的信息,以及树根方面的值就行了。
X快速前缀树的删除
找到待删除节点,然后删掉,重新维护叶子链表,回溯的时候从hash表里面删掉自己,对于单儿子的节点也要根据子树回溯即可。
- 本文作者: fightinggg
- 本文链接: http://fightinggg.github.io/yilia/yilia/Q7A61B.html
- 版权声明: 本博客所有文章除特别声明外,均采用 MIT 许可协议。转载请注明出处!



