ACM►老Blog迁移►blog►span

cf_468_B

题意

给你一个集合s
让你把这个集合划分为两个集合
在集合A中若x存在则a-x也存在
在集合B中若x存在则b-x也存在

数据范围

|s|<1e5
a<1e9
b<1e9

注意

集合中不包含相同的数

题解

使用并查集维护，
容易证明若x和a-x存在，则他们必定在同一个集合中
x和b-x同理

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<bits/stdc++.h>
using namespace std;

map<int,int>fa;
int find(int x){
    if(fa.find(x)==fa.end()) fa[x]=x;
    return x==fa[x]?x:fa[x]=find(fa[x]);
}
void join(int x,int y){
    int f1=find(x);
    int f2=find(y);
    if(f1>f2) swap(f1,f2); // f1
    fa[f1]=f2;
}

map<int,int>mp;
const int maxn=1e5+5;
int p[maxn];

int main(){
    int n,a,b;
    scanf("%d%d%d",&n,&a,&b);
    for(int i=1;i<=n;i++) {
        scanf("%d",p+i);
        mp[p[i]]++;
    }
    const int A=1e9+123;
    const int B=1e9+124;
    for(int i=1;i<=n;i++) {
        if(mp.find(a-p[i])!=mp.end()) join(p[i],a-p[i]);
        else join(p[i],B);
        if(mp.find(b-p[i])!=mp.end()) join(p[i],b-p[i]);
        else join(p[i],A);
    }
    if(find(A)==find(B)){
        printf("NO\n");
    }
    else{
        printf("YES\n");
        for(int i=1;i<=n;i++) {
            if(find(p[i])<=1e9) join(p[i],A);
            if(find(p[i])==A) printf("0 ");
            else printf("1 ");
        }
    }
}
ACM►学习笔记►数学

多项式

多项式

多项式在计算机中一般以数组方式储存，假设有一个多项式$f(x)$，并且$x^i$前面的系数为$a_i$，那么显然我们恰好可以用一个数组$a$来描述这个多项式， 多项式的系数$a_i$恰好存在数组$a$的第$i$项$a[i]$

多项式dft

在一般的多项式中，如果模数允许，乘法采取ntt来做，因为速度较快，多项式乘法是整个多项式体系的基石，他的常数如果太大，将影响到后面的所 有的多项式操作

多项式前期预处理

我们需要设置多项式最大长度，模数，原根，多项式最大长度的log，以及关键点reduce函数，传入一个-mod到mod之间的数x，返回x%mod,他比取模更快，然后是快速幂，在往后是复数i在模意义下的值，2i在模意义下的逆元,以及后面的逆元数组和他的初始化函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
const int maxn=100005<<2,mod = 998244353,g=3;// const 能明显加速代码
const int lgmaxn=20;
#define reduce(x) ((x)+(((x)>>31)&mod))

int qpow(int a,int b){
    int ret=1;
    while(b){
        if(b&1) ret=1ll*ret*a%mod;
        a=1ll*a*a%mod;
        b>>=1;
    }
    return ret;
}

int I=86583718;
int inv2=qpow(2,mod-2);
int inv2I=qpow(2*I,mod-2);

int inv[maxn]={1,1};
void inv_ini(){
    for(int i=2;i<maxn;++i) inv[i]=1ll*(mod-mod/i)*(inv[mod%i])%mod;
}

dft

蝴蝶变化必须预处理出来，否则太慢，最前面的是蝴蝶变换r[i][j]数组， 之后是ntt单位根wn数组和他的逆元数组。接着是ntt的数组的预处理函数以及ntt函数本体

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int allr[maxn<<1],*r[30],ntt_wn[30],ntt_revwn[30]; // 特别详细，没啥其他可说的 
//https://wenku.baidu.com/view/b438a51cce84b9d528ea81c758f5f61fb7362826.html
void dft_ini(){ // ntt 高性能
    r[0]=allr;
    for(int n=1,bit=0;n<maxn;n<<=1,bit++){
        for(int i=0;i<n;++i)r[bit][i]=(r[bit][i>>1]>>1)|((i&1)<<(bit-1));
        r[bit+1]=r[bit]+n;
        ntt_wn[bit]=qpow(g,(mod-1)>>bit);// 单位根
        ntt_revwn[bit]=qpow(ntt_wn[bit],mod-2);//逆变换则乘上逆元
    }
}
void dft(int*a,int n,int bits,int opt){ // ntt 
    for(int i=0;i<n;++i) if(i<r[bits][i]) swap(a[i],a[r[bits][i]]);
    for(int k=1,bit=0;k<n;k<<=1,bit++){
        int wn=opt==1?ntt_wn[bit+1]:ntt_revwn[bit+1];
        for (int i=0;i<n;i+=(k<<1)){
            for (int j=0,w=1; j<k; j++,w=1ll*w*wn%mod){
                int x=a[i+j], y=1ll*w*a[i+j+k]%mod;
                a[i+j]=reduce(x+y-mod), a[i+j+k]=reduce(x-y);
            }
        }
    }
    if(opt==-1) for(int i=0;i<n;++i) a[i]=1ll*a[i]*inv[n]%mod;
}//1800ms+

多项式拓展与对齐

为了后期代码可观性良好，以及少写一些奇怪的代码，poly_cpy(int*a,int n,int*b,int exn)提供了多项式拷贝等操作，即将一个多项式拷贝到另外一个多项式，必须保证exn>=n ，即先将a[0…n-1]拷贝到b[0…n-1] 然后把b数组多余的部分清零。这里如果ab为同一个数组，就不必进行拷贝了。

1
2
3
4
void poly_cpy(int*a,int n,int *b,int exn){//
    if(a!=b)  memcpy(b,a,sizeof(b[0])*n);
    if(n<exn) memset(b+n,0,sizeof(b[0])*(exn-n));
}

多项式乘法

为了防止常数问题，这里依旧采取最简单的方式，不让数组发生过多的拷贝，我们只实现a*=b这一个步骤，不实现c=a*b这种，很套路的乘法，先变为点指表示法 然后变为系数表示法即可

1
2
3
4
5
6
7
8
9
10
11
void poly_mul(int*a,int na,int*b,int nb){
    static int c[maxn];
    int exn=1,bits=0;
    while(exn<na+nb-1) exn<<=1,bits++;
    poly_cpy(a,na,a,exn);
    poly_cpy(b,nb,c,exn);
    dft(a,exn,bits,1);
    dft(c,exn,bits,1);
    for(int i=0;i<exn;i++) a[i]=1ll*a[i]*c[i]%mod;
    dft(a,exn,bits,-1);
}

多项式求逆

若两个多项式$f$和$g$，求出$f*g$然后让系数对mod取模，多项式忽略高于$x^k$次的项后等于1，则$f$和$g$互逆

这个地方很难以理解，因为有两个取模，所以会让很多初学者感到困惑，只要注意两个模是不同的，一个是系数对mod取模，另一个是多项式整体对$x^k$取模，即可

整个算法采取牛顿迭代法来完成，很容易被数学归纳法证明，$f(x)*g(x)===1(x^k,mod)$,当k等于1的时候，非常好得出结果，显然那时候g(x)至少需要 1项，即常数项，大于常数项的部分无效的，这个很容易证明，这一项等于$f(x)$的常数项的逆元。然后我们来根据$f(x)*g(x)===1(x^k,mod)$推出$f(x)g(x)===1(x^2k,mod)$ 的结果,以下是推导过程,显然$g(x)=g(x)(2-f(x)*g(x))$,只要自己注意一下项数的变化即可，然后我们倍增即可得出答案时间复杂度$T(n)=T(n/2)+nlg(n)$ 根据主定理$T(n)=O(nlgn)$img

1
2
3
4
5
6
7
8
9
10
11
12
13
void poly_inv(int*a,int n,int*b){ //  // %(x^n)  b(2-ab)
    static int c[maxn];
    if(n==1) {b[0]=qpow(a[0],mod-2); return;}
    poly_inv(a,(n+1)>>1,b);
    int exn=1,bits=0;
    while(exn<n+n-1) exn<<=1,bits++;
    poly_cpy(b,(n+1)>>1,b,exn);
    poly_cpy(a,n,c,exn);
    dft(b,exn,bits,1);
    dft(c,exn,bits,1);
    for(int i=0;i<exn;i++) b[i]=b[i]*(2-1ll*c[i]*b[i]%mod+mod)%mod;
    dft(b,exn,bits,-1);
}//p4738 开O2 500ms+ 洛谷最快200ms+

多项式除法

除法会有剩余，所以有两个返回值。

对于一个n-1次多项式f(x) 定义F(x)=x^nf(1/x) 则有以下推导img 余数直接ntt暴力即可

1
2
3
4
5
6
7
8
9
10
11
void poly_div(int*a,int na,int*b,int nb,int*c,int*d){
    reverse(a,a+na); reverse(b,b+nb);
    poly_inv(b,na-nb+1,c); //exn(2*na-2*nb+1)=exn(2*na-nb-nb+1)
    poly_mul(c,na-nb+1,a,na); //exn(na-nb+1+na-1)=exn(2*na-nb)
    reverse(a,a+na); reverse(b,b+nb);

    reverse(c,c+na-nb+1);
    poly_cpy(c,na-nb+1,d,na-nb+1);
    poly_mul(d,na-nb+1,b,nb);
    for(int i=0;i<na;i++) d[i]=reduce(a[i]-d[i]);
}// p4738 开O2 600ms+ 洛谷最快300ms+

多项式取对数

​ img
于是求导、求逆、乘、积分即可完成

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void poly_der(int*a,int n,int*b){ // 微分求导
    for(int i=1;i<n;i++) b[i-1]=1ll*a[i]*i%mod;
}

void poly_int(int*a,int n,int*b){ // 默认积分结果项常的数为0
    for(int i=1;i<=n;i++) b[i]=1ll*a[i-1]*inv[i]%mod;
    b[0]=0;
}


void poly_ln(int*a,int n,int*b){// a[exn(n+n-1)] //保证f(0)=1 , 默认积分结果项常的数为0 ，b[0]=ln(a[0])=1
    static int d[maxn];
    poly_der(a,n,d); // n-1 
    poly_inv(a,n,b); // n
    poly_mul(d,n-1,b,n);
    poly_int(d,n,b); // b[0]=ln(a[0])=ln(1)=0
}//p4725 开O2 700ms+ 洛谷最快300ms+

多项式求指数函数

​ 大佬已将讲的很清楚了，用泰勒展开求的img

1
2
3
4
5
6
7
8
9
10
void poly_exp(int*a,int n,int*b){//a[exn(n+n-1)] // 保证f(0)=0 b(1-ln(b)+f), 
    static int a_lnb[maxn];
    if(n==1) {b[0]=1;return;}
    poly_exp(a,(n+1)>>1,b);
    poly_cpy(b,(n+1)>>1,b,n);
    poly_ln(b,n,a_lnb);
    for(int i=0;i<n;++i) a_lnb[i]=reduce(a[i]-a_lnb[i]);
    a_lnb[0]=reduce(a_lnb[0]+1-mod);
    poly_mul(b,n,a_lnb,n);
}//p4726 开O2 1600ms+ 洛谷最快400ms+

多项式开根

​ 递归边界改为二次剩余即可img

1
2
3
4
5
6
7
8
9
10
void poly_sqrt(int*a,int n,int*b){//a[exn(n+n-1)] //保证a[0]=1, (b+a/b)/2 比上面那个好一些 
    static int c[maxn];
    if(n==1) {b[0]=1;return;}
    poly_sqrt(a,(n+1)>>1,b);
    poly_cpy(b,(n+1)>>1,b,n);
    poly_inv(b,n,c);
    poly_mul(c,n,a,n);
    int inv2=qpow(2,mod-2);
    for(int i=0;i<n;i++) b[i]=1ll*(b[i]+c[i])*inv2%mod;
}// P5205 开O2 3200+ms 洛谷最快600ms++

多项式快速幂

​ 先取对数，然后乘，然后取exp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void poly_pow(int *a,int n,int k,int *b){//a[exn(n+n-1)] // a^k not quick pow but quicker
    static int c[maxn],d[maxn];
    int t=0;
    while(t<n&&a[t]==0) t++;// a[t]*x^t
    if(1ll*t*k>=n)return; //k*t 居然能够爆int
    a+=t;// a/=x^t
    int invat=qpow(a[0],mod-2);
    int mul=qpow(a[0],k);
    for(int i=0;i<n-t;i++)d[i]=1ll*a[i]*invat%mod;
    for(int i=n-t;i<n;i++)d[i]=0;
    poly_ln(d,n,c);
    for(int i=1;i<n;i++)c[i]=1ll*c[i]*k%mod;
    poly_exp(c,n,b);
    for(int i=n-1;i>=1ll*t*k;i--) b[i]=1ll*b[i-1ll*k*t]*mul%mod;
    for(int i=1ll*k*t-1;i>=0;i--) b[i]=0;
    // b*=x^kt
}// 若k为大数，且保证a[0]=1，传入k%mod即可

多项式三角函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
void poly_sin(int*a,int n,int*b){//a[exn(n+n-1)]// 保证a[0]=0 -> c[0]=0 -> 可以exp
    static int c[maxn],d[maxn];
    for(int i=0;i<n;i++) c[i]=1ll*a[i]*I%mod;
    poly_exp(c,n,b);
    poly_inv(b,n,d);
    for(int i=0;i<n;i++) b[i]=1ll*(b[i]-d[i]+mod)*inv2I%mod;
} //  P5264 开O2 2111ms 洛谷最快691ms

void poly_cos(int*a,int n,int*b){//a[exn(n+n-1)]// 保证a[0]=0 -> c[0]=0 -> 可以exp
    static int c[maxn],d[maxn];
    for(int i=0;i<n;i++) c[i]=1ll*a[i]*I%mod;
    poly_exp(c,n,b);
    poly_inv(b,n,d);
    for(int i=0;i<n;i++) b[i]=1ll*(b[i]+d[i])*inv[2]%mod;
}//  P5264 开O2 2111ms 洛谷最快691ms

void poly_asin(int*a,int n,int*b){//a[exn(n+n-1)]// 保证a[0]=0 积分： f'/(sqrt(1-f*f))
    static int c[maxn];
    poly_cpy(a,n,b,n);// f
    poly_mul(b,n,b,n);// f*f
    b[0]=reduce(b[0]-1);// f*f-1 
    for(int i=0;i<n;i++)b[i]=mod-b[i]; //1-ff
    poly_sqrt_Strong(b,n,c);// sqrt(1-ff)
    poly_inv(c,n,b); // 1/sqrt(1-ff)
    poly_der(a,n,c);// f'
    poly_mul(c,n,b,n);//
    poly_int(c,n,b);// f'/(sqrt(1-f*f))
}// P5265 开O2 1626ms 洛谷最快985ms

void poly_atan(int*a,int n,int*b){//a[exn(n+n-1)] // 保证a[0]=0 积分： f'/(sqrt(1-f*f))
    static int c[maxn];
    poly_cpy(a,n,b,n);// f
    poly_mul(b,n,b,n);// f*f
    b[0]=reduce(b[0]+1-mod);// f*f+1 
    poly_inv(b,n,c); // 1/(f*f+1)
    poly_der(a,n,b);// f'
    poly_mul(c,n,b,n);//
    poly_int(c,n,b);// f'/(f*f+1)
}// P5265 开O2 1626ms 洛谷最快985ms

拉格朗日插值法

。。。。。。没啥可说的，存粹的套路

多项式多点求值

全家桶

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
#include<bits/stdc++.h>
using namespace std;

const int maxn=100005<<2,mod = 998244353,g=3;// const 能明显加速代码
const int lgmaxn=20;
#define reduce(x) ((x)+(((x)>>31)&mod))

int qpow(int a,int b){
    int ret=1;
    while(b){
        if(b&1) ret=1ll*ret*a%mod;
        a=1ll*a*a%mod;
        b>>=1;
    }
    return ret;
}

int I=86583718;
int inv2I=qpow(2*I,mod-2);

int inv[maxn]={1,1};
void inv_ini(){
    for(int i=2;i<maxn;++i) inv[i]=1ll*(mod-mod/i)*(inv[mod%i])%mod;
}

int allr[maxn<<1],*r[30],ntt_wn[30],ntt_revwn[30]; // 特别详细，没啥其他可说的 
//https://wenku.baidu.com/view/b438a51cce84b9d528ea81c758f5f61fb7362826.html
void dft_ini(){ // ntt 高性能
    r[0]=allr;
    for(int n=1,bit=0;n<maxn;n<<=1,bit++){
        for(int i=0;i<n;++i)r[bit][i]=(r[bit][i>>1]>>1)|((i&1)<<(bit-1));
        r[bit+1]=r[bit]+n;
        ntt_wn[bit]=qpow(g,(mod-1)>>bit);// 单位根
        ntt_revwn[bit]=qpow(ntt_wn[bit],mod-2);//逆变换则乘上逆元
    }
}
void dft(int*a,int n,int bits,int opt){ // ntt 
    for(int i=0;i<n;++i) if(i<r[bits][i]) swap(a[i],a[r[bits][i]]);
    for(int k=1,bit=0;k<n;k<<=1,bit++){
        int wn=opt==1?ntt_wn[bit+1]:ntt_revwn[bit+1];
        for (int i=0;i<n;i+=(k<<1)){
            for (int j=0,w=1; j<k; j++,w=1ll*w*wn%mod){
                int x=a[i+j], y=1ll*w*a[i+j+k]%mod;
                a[i+j]=reduce(x+y-mod), a[i+j+k]=reduce(x-y);
            }
        }
    }
    if(opt==-1) for(int i=0;i<n;++i) a[i]=1ll*a[i]*inv[n]%mod;
}//1800ms+

void poly_show(int*a,int n){
    for(int i=0;i<n;i++) printf(" %dx^%d +",a[i]>1000?a[i]-mod:a[i],i);
    cout<<endl;
}

void poly_cpy(int*a,int n,int *b,int exn){//
    if(a!=b)  memcpy(b,a,sizeof(b[0])*n);
    if(n<exn) memset(b+n,0,sizeof(b[0])*(exn-n));
}

/* 
 a会被作拓展，但是b不会，所以b的范围不会改变
 a[exn(na+nb-1)] 
 a*=b a和b允许是同一个数组
*/
void poly_mul(int*a,int na,int*b,int nb){
    static int c[maxn];
    int exn=1,bits=0;
    while(exn<na+nb-1) exn<<=1,bits++;
    poly_cpy(a,na,a,exn);
    poly_cpy(b,nb,c,exn);
    dft(a,exn,bits,1);
    dft(c,exn,bits,1);
    for(int i=0;i<exn;i++) a[i]=1ll*a[i]*c[i]%mod;
    dft(a,exn,bits,-1);
}
/*
b会被作拓展，但是a不会，所以a数组传入没有任何数组大小的要求
b[exn(n+n-1)]
*/
void poly_inv(int*a,int n,int*b){ //  // %(x^n)  b(2-ab)
    static int c[maxn];
    if(n==1) {b[0]=qpow(a[0],mod-2); return;}
    poly_inv(a,(n+1)>>1,b);
    int exn=1,bits=0;
    while(exn<n+n-1) exn<<=1,bits++;
    poly_cpy(b,(n+1)>>1,b,exn);
    poly_cpy(a,n,c,exn);
    dft(b,exn,bits,1);
    dft(c,exn,bits,1);
    for(int i=0;i<exn;i++) b[i]=b[i]*(2-1ll*c[i]*b[i]%mod+mod)%mod;
    dft(b,exn,bits,-1);
}//p4738 开O2 500ms+ 洛谷最快200ms+


/*
a/b=c...d
只有cb有要求exn(2*na-nb)
*/
void poly_div(int*a,int na,int*b,int nb,int*c,int*d){
    reverse(a,a+na); reverse(b,b+nb);
    poly_inv(b,na-nb+1,c); //exn(2*na-2*nb+1)=exn(2*na-nb-nb+1)
    poly_mul(c,na-nb+1,a,na); //exn(na-nb+1+na-1)=exn(2*na-nb)
    reverse(a,a+na); reverse(b,b+nb);

    reverse(c,c+na-nb+1);
    poly_cpy(c,na-nb+1,d,na-nb+1);
    poly_mul(d,na-nb+1,b,nb);
    for(int i=0;i<na;i++) d[i]=reduce(a[i]-d[i]);
}// p4738 开O2 600ms+ 洛谷最快300ms+

void poly_der(int*a,int n,int*b){ // 微分求导
    for(int i=1;i<n;i++) b[i-1]=1ll*a[i]*i%mod;
}

void poly_int(int*a,int n,int*b){ // 默认积分结果项常的数为0
    for(int i=1;i<=n;i++) b[i]=1ll*a[i-1]*inv[i]%mod;
    b[0]=0;
}


void poly_ln(int*a,int n,int*b){// a[exn(n+n-1)] //保证f(0)=1 , 默认积分结果项常的数为0 ，b[0]=ln(a[0])=1
    static int d[maxn];
    poly_der(a,n,d); // n-1 
    poly_inv(a,n,b); // n
    poly_mul(d,n-1,b,n);
    poly_int(d,n,b); // b[0]=ln(a[0])=ln(1)=0
}//p4725 开O2 700ms+ 洛谷最快300ms+

void poly_exp(int*a,int n,int*b){//a[exn(n+n-1)] // 保证f(0)=0 b(1-ln(b)+f), 
    static int a_lnb[maxn];
    if(n==1) {b[0]=1;return;}
    poly_exp(a,(n+1)>>1,b);
    poly_cpy(b,(n+1)>>1,b,n);
    poly_ln(b,n,a_lnb);
    for(int i=0;i<n;++i) a_lnb[i]=reduce(a[i]-a_lnb[i]);
    a_lnb[0]=reduce(a_lnb[0]+1-mod);
    poly_mul(b,n,a_lnb,n);
}//p4726 开O2 1600ms+ 洛谷最快400ms+

void poly_sqrt(int*a,int n,int*b){//a[exn(n+n-1)] //保证a[0]=1, (b+a/b)/2 比上面那个好一些 
    static int c[maxn];
    if(n==1) {b[0]=1;return;}
    poly_sqrt(a,(n+1)>>1,b);
    poly_cpy(b,(n+1)>>1,b,n);
    poly_inv(b,n,c);
    poly_mul(c,n,a,n);
    int inv2=qpow(2,mod-2);
    for(int i=0;i<n;i++) b[i]=1ll*(b[i]+c[i])*inv2%mod;
}// P5205 开O2 3200+ms 洛谷最快600ms++

int sqrt_residue(int a){ // return sqrt(a)
    int b=rand()%mod;   //找一个非二次剩余数 b
    while(qpow(b,(mod-1)>>1)!=mod-1) b=rand()%mod;
    int s=mod-1,t=0; // mod-1 =2^t*s = s<<t
    while(!(s&1)) s>>=1,t++;
    int inv=qpow(a,mod-2);
    int x,k;
    for(x=qpow(a,(s+1)>>1),k=1;t-k!=0;k++){ //
        int invxx=1ll*inv*x%mod*x%mod;
        if(qpow(invxx,1<<(t-k-1))==mod-1){
            x=1ll*x*qpow(b,s<<(k-1))%mod;
        }
    }
    return min(x,mod-x);
}

void poly_sqrt_Strong(int*a,int n,int*b){//a[exn(n+n-1)] //强化版 不保证a[0]=1 但保证a[0]为二次剩余
    static int c[maxn];
    if(n==1) {b[0]=sqrt_residue(a[0]);return;}// 其实就这一行不一样
    poly_sqrt_Strong(a,(n+1)>>1,b);
    poly_cpy(b,(n+1)>>1,b,n);
    poly_inv(b,n,c);
    poly_mul(c,n,a,n);
    for(int i=0;i<n;i++) b[i]=1ll*(b[i]+c[i])*inv[2]%mod;
}// 开O2跑1900ms+ 洛谷最快800ms++

void poly_pow(int *a,int n,int k,int *b){//a[exn(n+n-1)] // a^k not quick pow but quicker
    static int c[maxn],d[maxn];
    int t=0;
    while(t<n&&a[t]==0) t++;// a[t]*x^t
    if(1ll*t*k>=n)return; //k*t 居然能够爆int
    a+=t;// a/=x^t
    int invat=qpow(a[0],mod-2);
    int mul=qpow(a[0],k);
    for(int i=0;i<n-t;i++)d[i]=1ll*a[i]*invat%mod;
    for(int i=n-t;i<n;i++)d[i]=0;
    poly_ln(d,n,c);
    for(int i=1;i<n;i++)c[i]=1ll*c[i]*k%mod;
    poly_exp(c,n,b);
    for(int i=n-1;i>=1ll*t*k;i--) b[i]=1ll*b[i-1ll*k*t]*mul%mod;
    for(int i=1ll*k*t-1;i>=0;i--) b[i]=0;
    // b*=x^kt
}// 若k为大数，且保证a[0]=1，传入k%mod即可

void poly_sin(int*a,int n,int*b){//a[exn(n+n-1)]// 保证a[0]=0 -> c[0]=0 -> 可以exp
    static int c[maxn],d[maxn];
    for(int i=0;i<n;i++) c[i]=1ll*a[i]*I%mod;
    poly_exp(c,n,b);
    poly_inv(b,n,d);
    for(int i=0;i<n;i++) b[i]=1ll*(b[i]-d[i]+mod)*inv2I%mod;
} //  P5264 开O2 2111ms 洛谷最快691ms

void poly_cos(int*a,int n,int*b){//a[exn(n+n-1)]// 保证a[0]=0 -> c[0]=0 -> 可以exp
    static int c[maxn],d[maxn];
    for(int i=0;i<n;i++) c[i]=1ll*a[i]*I%mod;
    poly_exp(c,n,b);
    poly_inv(b,n,d);
    for(int i=0;i<n;i++) b[i]=1ll*(b[i]+d[i])*inv[2]%mod;
}//  P5264 开O2 2111ms 洛谷最快691ms

void poly_asin(int*a,int n,int*b){//a[exn(n+n-1)]// 保证a[0]=0 积分： f'/(sqrt(1-f*f))
    static int c[maxn];
    poly_cpy(a,n,b,n);// f
    poly_mul(b,n,b,n);// f*f
    b[0]=reduce(b[0]-1);// f*f-1 
    for(int i=0;i<n;i++)b[i]=mod-b[i]; //1-ff
    poly_sqrt_Strong(b,n,c);// sqrt(1-ff)
    poly_inv(c,n,b); // 1/sqrt(1-ff)
    poly_der(a,n,c);// f'
    poly_mul(c,n,b,n);//
    poly_int(c,n,b);// f'/(sqrt(1-f*f))
}// P5265 开O2 1626ms 洛谷最快985ms

void poly_atan(int*a,int n,int*b){//a[exn(n+n-1)] // 保证a[0]=0 积分： f'/(sqrt(1-f*f))
    static int c[maxn];
    poly_cpy(a,n,b,n);// f
    poly_mul(b,n,b,n);// f*f
    b[0]=reduce(b[0]+1-mod);// f*f+1 
    poly_inv(b,n,c); // 1/(f*f+1)
    poly_der(a,n,b);// f'
    poly_mul(c,n,b,n);//
    poly_int(c,n,b);// f'/(f*f+1)
}// P5265 开O2 1626ms 洛谷最快985ms

int*segtree[maxn<<2],segtreebuf[maxn*lgmaxn];
void zeropoint_to_poly(int rt,int*a,int n){ // T(n)=2*T(n/2)+nlg(n)= nlg(n)
    static int t1[maxn];
    if(rt==1) segtreebuf[0]=1;// auto ini
    segtree[rt]=segtreebuf+segtreebuf[0];
    segtreebuf[0]+=n+1;

    if(n==1) segtree[rt][0]=mod-a[0],segtree[rt][1]=1;
    else{
        int mid=n>>1;
        zeropoint_to_poly(rt<<1,a,mid);
        zeropoint_to_poly(rt<<1|1,a+mid,n-mid);
        poly_cpy(segtree[rt<<1],mid+1,t1,mid+1);
        poly_mul(t1,mid+1,segtree[rt<<1|1],n-mid+1);
        poly_cpy(t1,n+1,segtree[rt],n+1);
    }
}

/*
已知x0 x1 x2 ...
已知f(x)=a0x^0+a1x^1+a2x^2+...
求b0=f(x0),f(x1),f(x2)...
zeropoint_to_poly(1,)
*/
void poly_to_point(int rt,int*a,int n,int*b,int bn,int*c){ //T(n)=2*T(n/2)+nlg(n)=nlg(n)
    static int buf[maxn<<3],*d=buf,f[maxn];
    if(bn<=200&&n<=200){
        for(int i=0;i<bn;i++){
            c[i]=0;
            for(int j=n-1;j>=0;j--) c[i]=(1ll*c[i]*b[i]+a[j])%mod;
        }
    }
    else{
        d+=n<<2;
        if(n>bn) {
            poly_div(a,n,segtree[rt],bn+1,f,d);// nlg(n) 
            a=d; n=bn;
        }
        int mid=bn>>1;
        poly_to_point(rt<<1,a,n,b,mid,c);
        poly_to_point(rt<<1|1,a,n,b+mid,bn-mid,c+mid);
        d-=n<<2;
    }
}//时间卡边界上，不过刚刚好

//  拉格朗日插值法 
int facinv[maxn]={1,1};
void facinv_ini(){
    for(int i=0,fac=1;i<maxn;++i,fac=1ll*fac*i%mod) {
        facinv[i]=qpow(fac,mod-2);
    }
}

int lagrange(int*x,int*y,int n,int var){// y=f(x) 已知f(x0) f(x1) ... f(xn) 计算 f(var) O(n^2)
    int b=0;
    for(int i=0;i<=n;++i) {
        int t1=1,t2=1;
        for(int j=0;j<=n;j++){
            if(i==j) continue;
            t1=1ll*t1*(var -x[j]+mod)%mod;
            t2=1ll*t2*(x[i]-x[j]+mod)%mod;
        }
        int invt2=qpow(t2,mod-2);
        b=(b+1ll*y[i]*t1%mod*invt2)%mod;
    }
    return b;
}


int lagrange(int *y,int n,int x){// O(n) n次多项式有n+1项 y[0]...y[n] -> y[x]
    static int prepre[maxn],suf[maxn],*pre=prepre+1;
    pre[-1]=suf[n+1]=1;
    for(int i=0;i<=n;++i) pre[i]=1ll*pre[i-1]*(x-i+mod)%mod;
    for(int i=n;i>=0;i--) suf[i]=1ll*suf[i+1]*(i-x+mod)%mod;
    int b=0;
    for(int i=0;i<=n;++i) {
        int up=1ll*pre[i-1]*suf[i+1]%mod;
        int down=1ll*facinv[i]*facinv[n-i]%mod;
        b=(b+1ll*y[i]*up%mod*down)%mod;
    }
    return b;
}

// 
void lagrange_dfs(int rt,int*x,int n,int*g,int*a){
    static int buf[maxn<<4],*b=buf;
    b+=n<<2;
    if(n==1) a[0]=g[0];
    else{
        int mid=n>>1;
        lagrange_dfs(rt<<1,x,mid,g,a);
        lagrange_dfs(rt<<1|1,x+mid,n-mid,g+mid,b);
        poly_mul(a,mid,segtree[rt<<1|1],n-mid+1);
        poly_mul(b,n-mid,segtree[rt<<1],mid+1);
        for(int i=0;i<n;i++) a[i]=reduce(a[i]+b[i]-mod);
    }
    b-=n<<2;
}

void lagrange(int*x,int*y,int n,int *a){ // 多项式插值到系数表示法
    static int b[maxn],c[maxn]; // yi/gi*pord(x-xj) j!=i
    zeropoint_to_poly(1,x,n);
    poly_der(segtree[1],n+1,b);// b-> h'
    poly_to_point(1,b,n,x,n,c);//c->h'(x) 多点求值 洛必达法则
    for(int i=0;i<n;i++) c[i]=1ll*y[i]*qpow(c[i],mod-2)%mod;
    zeropoint_to_poly(1,x,n);
    lagrange_dfs(1,x,n,c,a);
}

inline int read(){
    register int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
    return (f==1)?x:-x;
}


int a[maxn],b[maxn],c[maxn],x[maxn],y[maxn];
int main(){
    dft_ini();inv_ini(); // all_poly
    // facinv_ini();// 简单的lagrange需要，复杂的不需要

    int n=read();
    for(int i=0;i<n;++i) a[i]=read();
    poly_ln(a,n,b);
    for(int i=0;i<n;i++) printf("%d ",b[i]);
}
ACM►学习笔记►数学

积性函数

积性函数

对于一个离散函数$f(x), x\in Z^+$ , 如果$\forall \gcd(a,b)=1$都有$f(a\cdot b)=f(a)\cdot f(b)$, 则称函数$f(x)$为积性函数。

完全积性函数

对于一个离散函数$f(x), x\in Z^+$ , 如果$\forall a,b\in Z^+$都有$f(a\cdot b)=f(a)\cdot f(b)$, 则称函数$f(x)$为完全积性函数。

积性函数分析

我们根据积性函数的定义，其实只要我们计算出了所有素数的幂的函数值，则任何其他$f(x)$都可以快速获取。

对此笔者准备了一个模版，我们只需要修改其中的56到63行即可

欧拉函数

$\phi(n)$就是小于等于n，且与n互质的数的个数。

1
2
3
4
5
6
7
8
9
10
11
12
//O(lgn)适用于少求
int euler(int n){
    int ret=n;
    for(int i=2; i*i<=n; i++)
        if(n%i==0){
            ret=ret-ret/i;
            do n/=i;
            while(n%i==0);
        }
    if(n>1)ret=ret-ret/n;
    return ret;
}

莫比乌斯函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//求单个值
ll getmob(ll a){
    ll x=a,tmp=a;
    int cnt=0,now=0;
    for(ll j=2;j*j<=x;j++){
        now=0;
        if(x%j==0){
            while(x%j==0) now++,x/=j;
            if(now>1) return 0;
            cnt++;
        }
    }
    if(x!=1) cnt++;
    return (cnt&1)?-1:1;
}
int getmu(int n)
{
    int v=1;
    for(int i=2;i*i<=n;i++)
     if(n%i==0)
     {
        v=-v;n/=i;
        if(n%i==0)return 0;
     }
    if(n!=1)v=-v;
    return v;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include<bits/stdc++.h>
using namespace std;

/*                        数论函数表
 i phi(i) PHI(i) muu(i) MUU(i) ddd(i) DDD(i) sig(i) SIG(i)
 1   1      1      1      1      1      1      1      1
 2   1      2     -1      0      2      3      3      4
 3   2      4     -1     -1      2      5      4      8
 4   2      6      0     -1      3      8      7     15
 5   4     10     -1     -2      2     10      6     21
 6   2     12      1     -1      4     14     12     33
 7   6     18     -1     -2      2     16      8     41
 8   4     22      0     -2      4     20     15     56
 9   6     28      0     -2      3     23     13     69
10   4     32      1     -1      4     27     18     87
11  10     42     -1     -2      2     29     12     99
12   4     46      0     -2      6     35     28    127
13  12     58     -1     -3      2     37     14    141
14   6     64      1     -2      4     41     24    165
15   8     72      1     -1      4     45     24    189
16   8     80      0     -1      5     50     31    220
17  16     96     -1     -2      2     52     18    238
18   6    102      0     -2      6     58     39    277
19  18    120     -1     -3      2     60     20    297
20   8    128      0     -3      6     66     42    339
21  12    140      1     -2      4     70     32    371
22  10    150      1     -1      4     74     36    407
23  22    172     -1     -2      2     76     24    431
24   8    180      0     -2      8     84     60    491
25  20    200      0     -2      3     87     31    522
26  12    212      1     -1      4     91     42    564
27  18    230      0     -1      4     95     40    604
28  12    242      0     -1      6    101     56    660
29  28    270     -1     -2      2    103     30    690
30   8    278     -1     -3      8    111     72    762*/

/****  * 超级积性函数线性筛 *  ****/
typedef long long ll;
const ll maxn=5e6;
ll no_pri[maxn]={0,1,0},pri[maxn],low[maxn];
ll PHI[maxn],DDD[maxn],XDX[maxn],MUU[maxn],SIG[maxn];
void f_ini(){
    for(ll i=2;i<maxn;i++){
        if(!no_pri[i]) low[i]=pri[++pri[0]]=i;
        for(ll j=1;pri[j]*i<maxn;j++){
            no_pri[pri[j]*i]=1;
            if(i%pri[j]==0) {
                low[pri[j]*i]=low[i]*pri[j];
                break;
            }
            else low[pri[j]*i]=pri[j];
        }
    }

    DDD[1]=PHI[1]=MUU[1]=SIG[1]=1;// 改这里
    for(ll i=1;i<=pri[0];i++){
        for(ll mul=pri[i],ct=1;mul<maxn;mul*=pri[i],ct++){
            DDD[mul]=ct+1;// 改这里
            SIG[mul]=SIG[mul/pri[i]]+mul;// 改这里
            MUU[mul]=ct==1?-1:0;// 改这里
            PHI[mul]=mul/pri[i]*(pri[i]-1);// 改这里
        }
    }

    for(ll i=2;i<maxn;i++){
        for(ll j=1;pri[j]*i<maxn;j++){
            ll x=low[i*pri[j]], y=i*pri[j]/x;
            DDD[x*y]=DDD[x]*DDD[y];
            MUU[x*y]=MUU[x]*MUU[y];
            PHI[x*y]=PHI[x]*PHI[y];
            SIG[x*y]=SIG[x]*SIG[y];
            if(i%pri[j]==0) break;
        }
    }

    for(ll i=1;i<maxn;i++) {
        DDD[i]+=DDD[i-1];
        MUU[i]+=MUU[i-1];
        PHI[i]+=PHI[i-1];
        SIG[i]+=SIG[i-1];
        XDX[i]=(DDD[i]-DDD[i-1])*i+XDX[i-1];
    }
}

int main(){
    f_ini();
    printf("数论函数表\n");
    printf(" i phi(i) PHI(i) muu(i) MUU(i) ddd(i) DDD(i) sig(i) SIG(i)\n");
    for(ll i=1;i<=30;i++) {
        printf("%2lld %3lld %6lld %6lld %6lld %6lld %6lld %6lld %6lld\n",i,PHI[i]-PHI[i-1],PHI[i],MUU[i]-MUU[i-1],MUU[i],DDD[i]-DDD[i-1],DDD[i],SIG[i]-SIG[i-1],SIG[i]);
    }
    return 0;
}
ACM►学习笔记►算法

递归大数

很早就想写这个了，觉得好厉害，结果分析停留在理论上，其实时间复杂度贼高

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include<bits/stdc++.h>
using namespace std;

struct big0{//最大999999，
    int o,h,l;// 溢出6位 高3位 低3位
    big0(){}
    big0(int rhs):o(0),h(0),l(rhs){}
    big0(int h,int l):o(0),h(h),l(l){}

    operator int(){return int(l);}
    big0 operator!=(const big0&rhs){return h!=rhs.h||l!=rhs.l;}
    big0 operator+(const big0&rhs){
        big0 ret=0;
        ret.l=l+rhs.l;
        ret.h=h+rhs.h+ret.l/1000;//进位
        ret.o=o+rhs.o+ret.h/1000;//暂时记录高位溢出情况
        ret.l%=1000;
        ret.h%=1000;
        return ret;
    }
    void show(int flag){
        printf("%03d%03d",h,l);
        // printf(" %3d %3d",h,l);
    }
    void show(){
        if(h!=0){
            printf("%d%03d",h,l);
        }
        else printf("%d",l);
    }

};

template<class T>
struct big{
    T o,h,l;// 溢出6位 高3位 低3位
    big(){}
    big(int rhs):o(0),h(0),l(rhs){}
    big(T h,T l):o(0),h(h),l(l){}

    operator int(){return int(l);}
    big operator!=(big rhs){return h!=rhs.h||l!=rhs.l;}
    big operator+(const big rhs){
        big ret=0;
        ret.l=l+rhs.l;
        ret.h=h+rhs.h+T(0,ret.l.o);
        ret.o=o+rhs.o+T(0,ret.h.o);
        ret.l.o=0;
        ret.h.o=0;
        return ret;
    }
    void show(int flag){
        h.show(1);
        l.show(1);
    }
    void show(){
        if(h!=T(0)){
            h.show();
            l.show(1);
        }
        else l.show();
    }
};

//big0  w<1e3   3*2^0
typedef big<big<big<big<big0>>>> big4;// w<1e(3*2^4)
typedef big<big<big<big<big4>>>> big8;// w<1e(3*2^8)
big8 a,b,c;

int main(){
    a=1;
    b=1;
    for(int i=3;i<=700;i++){
        c=a+b;
        a=b;
        b=c;
        printf("%3d: ",i);
        c.show();
        cout<<endl;
    }
}

输出了斐波拉契700位，数据还行，就是太慢了。

ACM►学习笔记►图论

Tarjan联通算法

强联通

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
struct Tarjan:Graph{//强连通分量缩点
    int low[maxn],dfn[maxn],belong[maxn],stk[maxn],instk[maxn],block[maxn];
    int step,color;
    void tarjan(){
        step=color=0;
        for(int i=0;i<=n;i++) dfn[i]=0;
        for(int i=1;i<=n;i++) if(dfn[i]==0) tarjan(i,0);//多个联通快
    }
    void tarjan(int u,int father=0){//此函数不开放
        low[u]=dfn[u]=++step; stk[++stk[0]]=u;instk[u]=1;
        for(int i=head[u];~i;i=edge[i].nex){
            int v=edge[i].v;
            if(dfn[v]) {
                if(instk[v]) low[u]=min(low[u],dfn[v]);
            }
            else{
                tarjan(v,u);
                low[u]=min(low[u],low[v]);
            }
        }
        if(low[u]==dfn[u]){
            block[color+1]=1;
            while(stk[stk[0]]!=u) {
                belong[stk[stk[0]]]=color+1;
                instk[stk[stk[0]--]]=0;
                block[color+1]++;
            }
            belong[stk[stk[0]]]=++color;
            instk[stk[stk[0]--]]=0;
        }
    }
    void rebuild(Dag&dag){
        set<long long>se;
        dag.ini(color);
        for(int u=1;u<=n;u++){
            int uu=belong[u];
            for(int i=head[u];~i;i=edge[i].nex){
                int v=edge[i].v;
                int vv=belong[v];
                if(uu==vv||se.find(uu*1e6+vv)!=se.end())continue;
                se.insert(uu*1e6+vv);
                dag.add_edge(uu,vv);
            }
            dag.dp[uu][u]=1;
            dag.w[uu]=block[uu];
        }
    }
}graph;

点双联通

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
struct Graph{
    static const int maxn=1e5+5, maxm=3e5+5;
    struct star{int v,nex;}edge[maxm<<1];
    int head[maxn],cnt,n;
    void ini(int n){
        this->n=n; cnt=-1;
        for(int i=0;i<=n;i++) head[i]=-1;
    }
    void add_edge(int u,int v){
        edge[++cnt]=star{v,head[u]}; head[u]=cnt;
        edge[++cnt]=star{u,head[v]}; head[v]=cnt;
    }
}tree;

struct Tarjan:Graph{//割点
    int low[maxn],dfn[maxn],cut[maxn];
    int step;
    void tarjan(){
        step=0;
        for(int i=0;i<=n;i++) dfn[i]=cut[i]=0;
        for(int i=1;i<=n;i++) if(dfn[i]==0) tarjan(i,0);//多个联通快
    }
    void tarjan(int u,int father=0){//此函数不开放
        low[u]=dfn[u]=++step;
        int first=1, son=0;
        for(int i=head[u];~i;i=edge[i].nex){
            int v=edge[i].v;
            if(v==father&&!first) first=false;
            else if(dfn[v]) low[u]=min(low[u],dfn[v]);
            else{
                son++;
                tarjan(v,u);
                low[u]=min(low[u],low[v]);
                //一个顶点u是割点,当且仅当1或2
                //1.u为树根且u有多与一个子树
                //2.u不为树根且存在边(u,v)为树边，使得dfn[u]<=low[v]
                if(father!=0&&dfn[u]<=low[v]) cut[u]=1;
                if(father==0&&son>1) cut[u]=1;
            }
        }
    }
}graph;

边双联通

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
struct Graph{
    static const int maxn=1e5+5, maxm=3e5+5;
    struct star{int v,nex;}edge[maxm<<1];
    int head[maxn],cnt;
    void ini(int n){
        for(int i=0;i<=n;i++) head[i]=-1;
        cnt=-1;
    }
    void add_edge(int u,int v){
        edge[++cnt]=star{v,head[u]};
        head[u]=cnt;
        edge[++cnt]=star{u,head[v]};
        head[v]=cnt;
    }
};

struct Tarjan:Graph{//双联通分量, 割边, 桥, 边双联通缩点
    struct Bridge{int u,v;}bridge[maxn];
    int dfn[maxn],low[maxn],belong[maxn],vis[maxn],sta[maxn],sta_,nums,bridge_;
    void ini(int n){
        for(int i=0;i<=n;i++) vis[i]=0;
        bridge_=0;
        nums=0;
        Graph::ini(n);
    }
    void tarjan(int u,int father,int&step){
        low[u]=dfn[u]=++step;
        sta[++sta_]=u;
        vis[u]=1;
        bool firsttimes=true;//用于判重边
        for(int i=head[u];~i;i=edge[i].nex){
            int v=edge[i].v;
            if(v==father&&firsttimes) {
                firsttimes=false;
                continue;
            }//父边
            if(vis[v]==1) low[u]=min(low[u],dfn[v]);//回边,终点在栈中
            else {//树边
                tarjan(v,u,step);
                low[u]=min(low[u],low[v]);
                if(low[v]>dfn[u]) bridge[++bridge_]=Bridge{u,v};
            }
        }
        if(low[u]==dfn[u]){
            while(sta[sta_]!=u) belong[sta[sta_--]]=nums+1;
            belong[sta[sta_--]]=++nums;
        }
    }
}graph;
ACM►学习笔记►图论

LCA 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
struct Graph{
    static const int maxn=1e5+5, maxm=3e5+5;
    struct star{int v,nex;}edge[maxm<<1];
    int head[maxn],cnt;
    void ini(int n){
        for(int i=0;i<=n;i++) head[i]=-1;
        cnt=-1;
    }
    void add_edge(int u,int v){
        edge[++cnt]=star{v,head[u]};
        head[u]=cnt;
        edge[++cnt]=star{u,head[v]};
        head[v]=cnt;
    }
};

struct Lca:Graph{// 不要忘记ini
    int dep[maxn],dad[maxn],siz[maxn],son[maxn],chain[maxn],dfn[maxn];
    void dfs1(int u,int father){//dfs1(1,0)
        dep[u]=dep[father]+1;//ini
        dad[u]=father;
        siz[u]=1;
        son[u]=-1;
        for(int i=head[u];~i;i=edge[i].nex){
            int v=edge[i].v;
            if(v==father)continue;
            dfs1(v,u);
            siz[u]+=siz[v];
            if(son[u]==-1||siz[son[u]]<siz[v]) son[u]=v;
        }
    }
    void dfs2(int u,int s,int&step){
        dfn[u]=++step;
        chain[u]=s;
        if(son[u]!=-1) dfs2(son[u],s,step);
        for(int i=head[u];~i;i=edge[i].nex){
            int v=edge[i].v;
            if(v!=son[u]&&v!=dad[u]) dfs2(v,v,step);
        }
    }
    int lca(int x,int y){
        while(chain[x]!=chain[y]){
            if(dep[chain[x]]<dep[chain[y]]) swap(x,y);//dep[chain[x]]>dep[chain[y]]
            x=dad[chain[x]];
        }
        return dep[x]<dep[y]?x:y;
    }
}tree;
计算机组成原理

虚拟内存

程序跑起来都是跟地址相关的，可以试想，如果多个程序一起跑，难道不相互影响吗？又或者说 为什么我们写代码，从不去关心我们的程序在哪里运行？大家都用一个Memory，为什么没有相互破坏？好神奇！！

为了让多个程序在同一台计算机上更好的运行，而不发生相互破坏性影响，虚拟内存的概念被提了出来，从此多个程序都有了独立的地址空间。

虚拟内存，是与物理内存相对应的，可以设想，我们程序a运行起来，写地址Mx1，程序b运行起来 也写Mx1，结果是，他们没有相互影响，为什么？因为这个地址Mx1是虚拟内存，是假的，程序a的mx1 和程序b的mx1不是同一个地址，程序a写Mx1，结果写到哪去了呢？我们不知道，这件事是操作系统 完成的，他把程序a的Mx1映射到了一个地方，又把程序b的Mx1映射到了另一个地方，这两个程序就能 独立的跑起来了。

解决上述问题的方法很简单，是有一个叫做页表的东西来完成的。

内存分页

为了更好的解决这个问题，我们将内存分页，就成了多个page，假设一个page有16KB，那么page里面的 地址就有16KB=2^14B,个地址，我们需要用14bits来表示这个地址，所以，基于这种page模式 地址的低14位就是page offset，页偏移量，其他的高位叫做page number，在虚拟内存里面 叫做Virutal page number,在物理内存里面叫做Physical page number ,注意物理内存和虚拟内存 的page offset是一样的。于是我们一个page一个page的映射，一次映射就是一整页。页内部保持地址 一致，地址映射只是page number变化。

页表

我们之前说过，操作系统进行了一次映射，这个映射是怎么完成的呢？于是叶表出来了，有一张表 记录了所有虚拟内存地址页号（vpn）到物理内存地址页号的（ppn）的所有信息，显然为了高效性 这里我们使用数组来完成，在c++里面如果有一个数组a[4]={1,2,0,3};那么就有a[0]=1,a[1]=2,a[2]=0, a[3]=3;ok 映射完成了！！O（1）映射，高性能。但是还是有一个问题。这个数组可能回究极大大大大。 设想一个64GB的物理内存，以及1024GB的虚拟内存，页大小16KB，那么会导致36位的 physical address 40位的virtual address 以及14位的page offset，然后我们发现physical page number 达到了22位，virtual page number 达到了26位，我们来算一下这个数组有多大，26位的元素，2^26*22？bit，大概是150MB左右 这么大，缓存也放不下呀，只能放内存里面，可是这这东西读取频率是究极高的，放内存里面读写太慢了。

Translation Look-Aside Buffers (TLBs)

​ 于是我们思考能不能把一部分经常要用到放到Cache里面？能啊！！为什么不能？为了让叶表用的更加得劲， 我们还专门给你弄一个Cache，重新取名位TLB。哈哈。TLB和普通Cache一样，page offset和 TLB index TLB tag和Cache的一摸一样，计算方法一摸一样，此处不再多言。

TLB Entry

​ 这也是一样的，只是多一个Access Control (一般 2 bits),也就多两位来着。Cache懂了这里很简单。

计算机组成原理

补码

我们用数学方式来重新定义计算机里面的运算，因为内存是有限的，所以我们在计算机当中 存储数据的时候，这些数据都是有范围的数，所以所有的运算都是建立在模数上的，例如加法成了 模加。a+b成了（a+b）%mod。
为了让减法跑的更快，我们把减法丢掉了，于是这个世界只有加法了。减法成了加一个负数。 负数又是怎么定义的呢？如果x=-1，我们可以这样来存储（0-1+mod）%mod=mod-1 于是我们把负数也映射到了新的正数上。
由于模加也满足加法的交换率结合律等等优良性质。很明显，对于负数-x和-y我们存的是mod-x 和mod-y，于是经历模加（-x+-y）%mod=（mod-x+mod-y)%mod这显然是正确的。

计算机组成原理

浅谈缓存

# Cache的基本理论指导

​ 由于计算机内部memery与 processor之间的速度差距过大，导致计算机整体速度降低，memery拖慢了速度。于是人们想出 了一个办法来解决他。缓存Cache诞生了。
​ Cache相对于Memery来说，速度快了很多，速度快意味着造价高，容量小，这是代价，我们没有那么多钱来用Cache来当作 Memery，于是我们尝试，让他作为Processor与Memery的中介。
​ 为什么要Cache，因为Memery太慢了，用Cache的话，容量问题很显然，Cache很小，没有Memery那么大。但是我们的初衷 是什么，用Cache去代替Memery，但是，Cache这个家伙小啊，我们不可能把一个大的东西放进一个小的盒子里面。 这是缓存 面临的最大问题。
​ 重新思考计算机的运转，指令是一条一条执行的，当计算机运转的时候，CPU关心的不是整个Memery，他只要他的东西，他所需要的 只是局部的信息。于是我们开始思考，既然Cache没有Memery那么大，那我们就构建一个一对多的映射，一个Cache地址，去对应 多个Memery地址，问题似乎解决了，是的Cache就是那样工作的。
​ 一对多的问题不好解决，你怎么知道一对多的时候，对应的是哪一个呢？我们是这样子解决的，把Memery的地址映射 Mx到Cache的地址Cx，这是唯一的，但是Cache是一对多啊，我们假设是一对四，然后我们在Cache的地址所指向的位置添 加一个标记，用来指示他目前对应是哪一个Memery地址，不妨说他目前对应的是第三个Memery。现在问题基本解决了。 例如：
​ 有四个Memery地址Mx1，Mx2，Mx3，Mx4，都映射到了Cx，但是Cx上有一个标记，标记说Cx目前存的值等于Mx3 存的值。这样就完美解决了映射的问题。但是新的问题来了，无法逃避，Cache毕竟没有Memery那么大，我现在 要访问Mx1，结果我找到了Cx，Cx却告诉我他现在存的东西不是Mx1，而是Mx3，怎么办？？
​ 没办法，这种情况叫miss，只能从Memery找了，我们是这样做的：把从Memery把Mx1以及他附近的其他东西搬过来 搬到Cache，然后更新Cache的标志。回到刚才的例子，也就是把Mx1以及他附近的其他信息的东西搬到了Cx上 然后改掉Cx的标记，说Cx现在不是Mx3了，他现在与Mx1一起了。
​ 如此复杂的操作，真的回使得计算机变快吗？是的，平均性能上提高了，因为Cache和Memery速度差异巨大。不过杨老师曾指出一个 反例，他说，你要是有个恐怖分子，不用我们的Cache，当Cx与Mx1一致的时候你要用Mx2，当Cx变得根Mx2相同了，你 又要用Mx1，那岂不是凉凉？好像确实是这样子的。
​ 为什么说是平均性能的提高呢？有两点，memery使用的时间局部性和空间局部性，当你使用了一个Memery的地址 后，你在不久的将来可能还会使用他 ，你也有肯能使用他附近的其他信息。所以我们把和他相关的东西一股脑都放进 Cache就可以了，但是放多少呢？这个问题，先辈们已经通过统计得出来结论。我们不必关心。

Cache的基本实际实现

​ 之前我们谈到的只是口糊，具体实现的时候，不是一个地址对应一个地址，而是一块对应一块（block）， 我们曾谈到，空间局部性，所以说这里不要一个地址对应一个地址的玩了。我们引入block。也就是说 我们把地址Mx1_begin 到Mx1_end这一整块的地址映射到Cx_begin到Cx_end ， 然后放一个标记就可以了， 这样的优点很多，比如说省掉了很多标记的记录。。。等等的
​ Cache的地址分为三大块，tag,index,和offset
​ offset指的是一种偏移量，我们之前说过，Cache里面分了很多个block，每一个block都是一个整体，所以 当我们找到了正确的当block当时候，offset用来指向block里面的详细地址。显然，block里面有多少种地址 offset就有多少种值。举个例子，当block是64B的时候，他一共有2^6个byte，我们计算机寻址所关心的只是 哪一个byte，（一般而言，四个byte为一个words）所以我们的offset需要有6个bit，才能恰好指向这2^6个 byte。于是在这种情况下offset为6位
​ index指向我们要找的哪一个block，见杨老师的图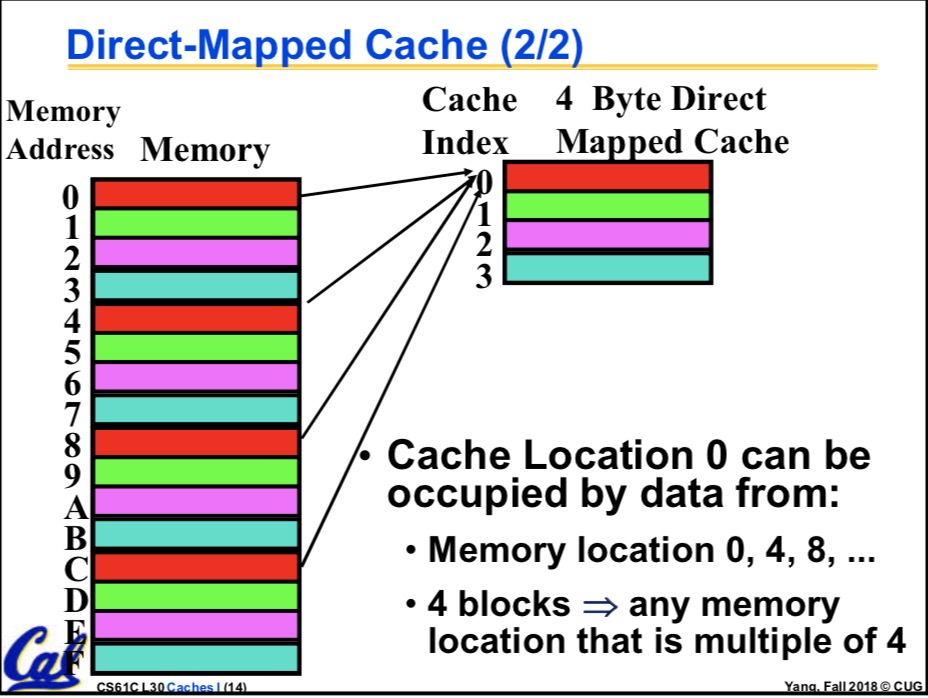

​ 很明显，如果在上述条件下我们的Cache一共有64KB的话，那我们就有 64KB/6B=2^10个block，于是index就是10位的了，可是有一些Cache，特别的有趣，它允许多对多。这就很 头疼了，不过这确实是个好办法。有一定的优点。 多对多是个什么情况呢？类似于这样,有Cx1 Cx2，Mx1，Mx2，Mx3，Mx4，他们很乱，四个Mx都可能映射到 Cx1，也都可能映射到Cx2，注意对比之前的一对多:有Cx，Mx1，Mx2，Mx3，Mx4,四个Mx都可能映射到Cx 多对多多优点的话，不好说，其实是我不知道。这种多对多的骚操作，实现起来更复杂了，他叫n-way set-assoc. 中文名n路集相关。很shit，很神奇。下面是二路集相关（还是杨老师的）.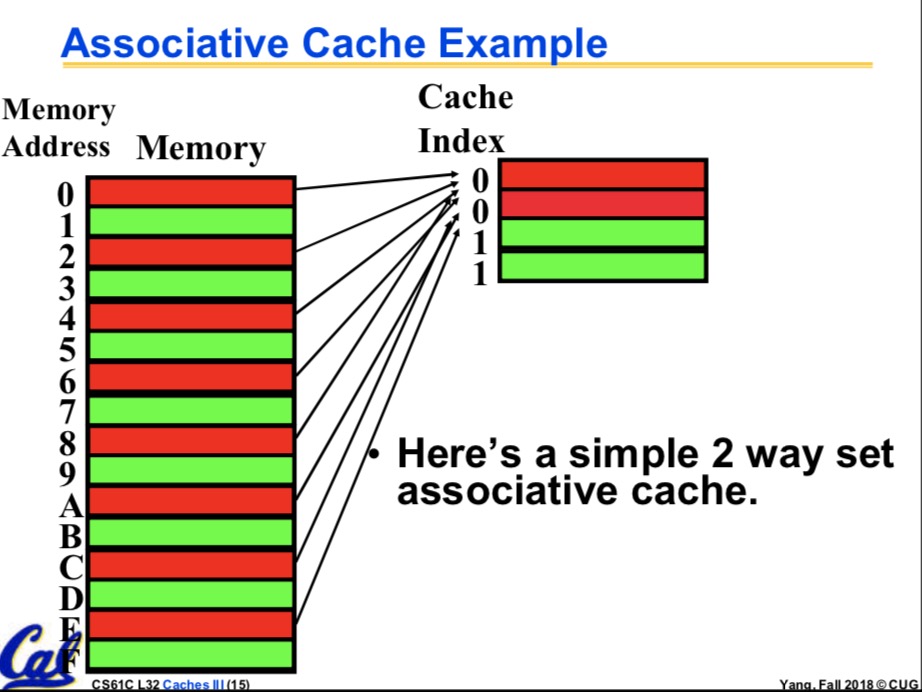

​ 在n路及相关的情况下，index又叫做set，这是他的新名字，这个时候他指向一堆block，换句话说，一堆block共用 一个index。于是，如果刚刚的64KBCache是二路集相关的话，他的index是9位，因为一个index可以指向两个 block。
​ 至于tag，我不是很清楚了。应对考试的话，他的位数用PPA(Physical Page Address )减去index和offset就得到了。
​ 最后剩下的一个是Data Cache entry 他的大小等于Valid bit, Dirty bit, Cache tag + ？？ Bytes of Data， 有这些一起组成。Valid bit 一般是一位，他的作用是用来指示这个block是否有用，为什么会没有用呢 我们想到，程序总有启动的时候，当程序刚刚启动的时候，block是无效的，它里面的数据存在，但是 数据却不一定和Memery保持一致。这个问题无法避免，但是可以通过Valid bit解决。Dirty bit是一种懒惰 标记，一般的树形结构，例如线段树，spaly，以及各种可持久化数据结构里面都用这种东西。他用来表明 一种懒惰性，因为Memery慢，因为Cache是用来代替Memery的，当我们读取数据的时候，没有他的用途 单当我们更新数据的时候，我们一定要立即更新Memery吗，不是的，我们可以只更新Cache的block，等 到miss发生的时候，在把它们一起写入Memery即可，所以他叫脏位。是一位。Cache tag就是我们之前说的 标记，用来防止一对多的情况下的那个标记，他等于前面我们算出来的tag的大小。最后一个是Bytes of Data 他恰好等于block的大小，例如64KB的那个Cache，他的大小位64KB=64*8bits=512bits，于是总大小为 1+1+21+512=535bits